题目内容
16.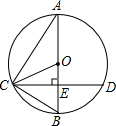 如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.(1)求证:∠ACO=∠BCD;
(2)若AE=18cm,CD=24cm,求⊙O的面积.
分析 (1)根据垂径定理得到$\widehat{BC}$=$\widehat{BD}$,根据同弧或等弧所对的圆周角相等,得到∠CAB=∠BCD,根据等腰三角形的性质得到答案;
(2)设⊙O的半径为R,根据勾股定理列出关于R的方程,解方程求出R,根据圆的面积公式计算即可.
解答 (1)证明:∵AB⊥CD,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠CAB=∠BCD,
∵OA=OC,
∴∠ACO=∠CAB,
∴∠ACO=∠BCD;
(2)解:设⊙O的半径为R,
则OE=18-R,
由勾股定理得,OC2=CE2+OE2,
即R2=122+(18-R)2,
解得,R=13,
∴⊙O的面积=169πcm2.
点评 本题考查的是垂径定理、圆周角定理和勾股定理的应用,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧以及同弧或等弧所对的圆周角相等是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
8.下列各组数作为三角形的边长,其中不能构成直角三角形的是( )
| A. | 6,8,10 | B. | 5,12,13 | C. | 3,4,5 | D. | 5,7,9 |
 如图,直线AB:y=kx+3过点(-2,4)与抛物线y=$\frac{1}{2}{x^2}$交于A、B两点;
如图,直线AB:y=kx+3过点(-2,4)与抛物线y=$\frac{1}{2}{x^2}$交于A、B两点; 如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2-4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.
如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2-4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长. 有一数值转换机,原理如图所示,若输入的x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2014次输出的结果是1.
有一数值转换机,原理如图所示,若输入的x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2014次输出的结果是1.