题目内容
6.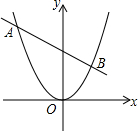 如图,直线AB:y=kx+3过点(-2,4)与抛物线y=$\frac{1}{2}{x^2}$交于A、B两点;
如图,直线AB:y=kx+3过点(-2,4)与抛物线y=$\frac{1}{2}{x^2}$交于A、B两点;(1)直接写出点A、点B的坐标;
(2)在直线AB的下方的抛物线上求点P,使△ABP的面积等于5.
分析 (1)把点(-2,4)代入直线AB:y=kx+3求得k,再与抛物线y=$\frac{1}{2}{x^2}$建立方程求得A、B两点;
(2)设出点P的横坐标为a,运用割补法用a的代数式表示△APB的面积,然后根据条件建立关于a的方程,从而求出a的值,进而求出点P的坐标.
解答 解:(1)∵把点(-2,4)代入直线AB:y=kx+3,解得k=-$\frac{1}{2}$,
∴直线的解析式为y=-$\frac{1}{2}$x+3.
联立方程得$\frac{1}{2}$x2=-$\frac{1}{2}$x+3,
解得:x=-3或x=2.
∴点A的坐标为(-3,$\frac{9}{2}$),点B的坐标为(2,2).
(2)过点P作PQ∥y轴,交AB于点Q,
过点A作AM⊥PQ,垂足为M,
过点B作BN⊥PQ,垂足为N,如图1所示.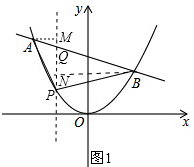
设点P的横坐标为a,则点Q的横坐标为a.
∴yP=$\frac{1}{2}$a2,yQ=-$\frac{1}{2}$a+3.
∵点P在直线AB下方,
∴PQ=yQ-yP
=-$\frac{1}{2}$a+3-$\frac{1}{2}$a2
∵AM+NB=a-(-3)+2-a=5.
∴S△APB=S△APQ+S△BPQ
=$\frac{1}{2}$PQ•AM+$\frac{1}{2}$PQ•BN
=$\frac{1}{2}$PQ•(AM+BN)
=$\frac{1}{2}$(-$\frac{1}{2}$a+3-$\frac{1}{2}$a2)•5
=5.
整理得:a2+a-2=0.
解得:a1=-2,a2=1.
当a=-2时,yP=$\frac{1}{2}$×(-2)2=2.
此时点P的坐标为(-2,2).
当a=1时,yP=$\frac{1}{2}$×12=$\frac{1}{2}$.
此时点P的坐标为(1,$\frac{1}{2}$).
∴符合要求的点P的坐标为(-2,2)或(1,$\frac{1}{2}$).
点评 此题考查一次函数与二次函数的交点问题,二次函数的性质,通过解方程组求两函数交点坐标、用割补法表示三角形的面积等方法,综合性比较强.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | (x-4)2=14 | B. | (x+4)2=14 | C. | (x+2)2=2 | D. | (x-2)2=2 |
| A. | x2-2=0 | B. | 2x3+3=5 | C. | $3x+\frac{1}{x}=4$ | D. | x+2y=4 |
| A. | -(-0.6$\stackrel{•}{6}$) | B. | π | C. | -$\frac{3}{5}$ | D. | 0.341 |
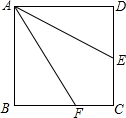 如图,已知E是正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE,那么AF,AD,CF三条线段的关系是( )
如图,已知E是正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE,那么AF,AD,CF三条线段的关系是( )| A. | AF>AD+CF | B. | AF<AD+CF | C. | AD=AF-CF | D. | 无法确定 |
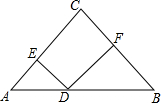 如图,在△ABC中,AC=BC=5,AB=8,D是AB边上的一动点(不与A、B重合),DE⊥AC,DF⊥BC,则FD+ED的值是4.8.
如图,在△ABC中,AC=BC=5,AB=8,D是AB边上的一动点(不与A、B重合),DE⊥AC,DF⊥BC,则FD+ED的值是4.8.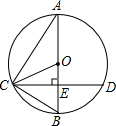 如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.