��Ŀ����
18����ֱ������ϵ�У����Dz����������꣬�������Ϊ�����ĵ��֮Ϊ���й��ᡱ����1������y=$\sqrt{3}$x+2��ͼ�������С��й��ᡱ�����ꣻ
��2��������y=$\frac{k}{x}$��k��0��kΪ��������ͼ��������ֻ���������й��ᡱ�����������k��ֵ����Ӧ���й��ᡱ�����ꣻ
��3�������κ���y=��k2-3k+2��x2+��2k2-4k+1��x+k2-k��kΪ��������ͼ����x���ཻ�õ�������ͬ�ġ��й��ᡱ�����ʸú�����ͼ����x����Χ�ɵ�ƽ��ͼ���У����߽磩��һ�������ж��ٸ����й��ᡱ��
���� ��1����Ϊx��������x��0ʱ��$\sqrt{3}$x��һ��������������x��0ʱ��$\sqrt{3}$x+2��������������x=0��y=2���ݴ��������y=$\sqrt{3}$x+2��ͼ�������С��й��ᡱ�����꼴�ɣ�
��2�������жϳ���k=1ʱ������y=$\frac{k}{x}$��k��0��kΪ��������ͼ��������ֻ���������й��ᡱ����1��1������-1��-1����Ȼ���жϳ���k��1ʱ������y=$\frac{k}{x}$��k��0��kΪ��������ͼ����������4�����й��ᡱ���ݴ��������k��ֵ����Ӧ���й��ᡱ�����꼴�ɣ�
��3�������k2-3k+2��x2+��2k2-4k+1��x+k2-k=0����[��k-1��x+k][��k-2��x+��k-1��]=0�����x1��x2��ֵ�Ƕ��٣�Ȼ�����x1��x2��ֵ�����������k��ֵ�Ƕ��٣������ݺ����꣬�������Ϊ�����ĵ��֮Ϊ���й��ᡱ���жϳ��ú�����ͼ����x����Χ�ɵ�ƽ��ͼ���У����߽磩��һ�������ж��ٸ����й��ᡱ���ɣ�
��� �⣺��1����x��������x��0ʱ��$\sqrt{3}$x��һ����������
��x��0ʱ��$\sqrt{3}$x+2����������
��x=0��y=2��
������y=$\sqrt{3}$x+2��ͼ���ϡ��й��ᡱ�������ǣ�0��2����
��2���ٵ�k=1ʱ������y=$\frac{k}{x}$��k��0��kΪ��������ͼ��������ֻ���������й��ᡱ��
��1��1������-1��-1����
�ڵ�k=-1ʱ������y=$\frac{k}{x}$��k��0��kΪ��������ͼ��������ֻ���������й��ᡱ��
��1��-1������-1��1����
�۵�k�١�1ʱ������y=$\frac{k}{x}$��k��0��kΪ��������ͼ����������4�����й��ᡱ��
��1��k������-1��-k������k��1������-k��-1�������뺯��y=$\frac{k}{x}$��k��0��kΪ��������ͼ��������ֻ���������й��ᡱì�ܣ�
���Ͽɵã�k=1ʱ������y=$\frac{k}{x}$��k��0��kΪ��������ͼ��������ֻ���������й��ᡱ����1��1������-1��-1����
k=-1ʱ������y=$\frac{k}{x}$��k��0��kΪ��������ͼ��������ֻ���������й��ᡱ����1��-1������-1��1����
��3���k2-3k+2��x2+��2k2-4k+1��x+k2-k=0��
��[��k-1��x+k][��k-2��x+��k-1��]=0��
��$\left\{\begin{array}{l}{{x}_{1}=\frac{k}{1-k}}\\{{x}_{2}=\frac{k-1}{2-k}}\end{array}\right.$
��k=$\frac{{x}_{1}}{{x}_{1}+1}=\frac{{2x}_{2}+1}{{x}_{2}+1}$��
�������ɵ�
x1x2+2x2+1=0��
��x2��x1+2��=-1��
��x1��x2����������
��$\left\{\begin{array}{l}{{x}_{2}=1}\\{{x}_{1}+2=-1}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{x}_{1}+2=1}\end{array}\right.$
��$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{x}_{2}=1}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{x}_{2}=-1}\end{array}\right.$
�ٵ�$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{x}_{2}=1}\end{array}\right.$ʱ��
��$\frac{k-1}{2-k}=1$��
��k=$\frac{3}{2}$��
�ڵ�$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{x}_{2}=-1}\end{array}\right.$ʱ��
��$\frac{k}{1-k}=-1$��
��k=k-1���⣻
���ϣ��ɵ�
k=$\frac{3}{2}$��x1=-3��x2=1��
y=��k2-3k+2��x2+��2k2-4k+1��x+k2-k
=[${��\frac{3}{2}��}^{\;}$2-3��$\frac{3}{2}$+2]x2+[2����$\frac{3}{2}$��2-4��$\frac{3}{2}$+1]x+��$\frac{3}{2}$��2-$\frac{3}{2}$
=-$\frac{1}{4}$x2-$\frac{1}{2}$x$+\frac{3}{4}$
�ٵ�x=-2ʱ��
y=-$\frac{1}{4}$x2-$\frac{1}{2}$x$+\frac{3}{4}$
=$-\frac{1}{4}$����-2��2$-\frac{1}{2}$����-2��+$\frac{3}{4}$
=$\frac{3}{4}$
�ڵ�x=-1ʱ��
y=-$\frac{1}{4}$x2-$\frac{1}{2}$x$+\frac{3}{4}$
=$-\frac{1}{4}$����-1��2$-\frac{1}{2}$����-1��+$\frac{3}{4}$
=1
�۵�x=0ʱ��y=$\frac{3}{4}$��
���⣬�ú�����ͼ����x����Χ�ɵ�ƽ��ͼ����x���ϵġ��й��ᡱ��3����
��-2��0������-1��0������0��0����
���ϣ��ɵ�
�����κ���y=��k2-3k+2��x2+��2k2-4k+1��x+k2-k��kΪ��������ͼ����x���ཻ�õ�������ͬ�ġ��й��ᡱ��
�ú�����ͼ����x����Χ�ɵ�ƽ��ͼ���У����߽磩��һ��������6�����й��ᡱ����-3��0������-2��0������-1��0����-1��1������0��0������1��0����
���� ��1��������Ҫ�����˷������������⣬�����˷�������˼���Ӧ�ã�Ҫ�������շ�����������ͼ������ʣ�
��2����������˶��¶��塰�й��ᡱ����������գ�������Ĺؼ���Ҫ��ȷ�������꣬�������Ϊ�����ĵ��֮Ϊ���й��ᡱ��

 ����ѧ����ϵ�д�
����ѧ����ϵ�д�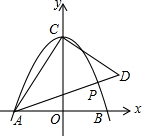 ��ͼ��������y=ax2+4��x�ύ��A��B���㣨A��B����ߣ�����y�ύ�ڵ�C��AB=4��
��ͼ��������y=ax2+4��x�ύ��A��B���㣨A��B����ߣ�����y�ύ�ڵ�C��AB=4�� �躯��y=��x-1��[��k-1��x+��k-3��]��k�dz�������
�躯��y=��x-1��[��k-1��x+��k-3��]��k�dz�������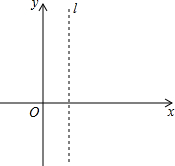 ��֪������y=-x2+bx+c��x�ύ�ڵ�A��m-2��0����B��2m+1��0������A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪP���Գ���Ϊl��x=1��
��֪������y=-x2+bx+c��x�ύ�ڵ�A��m-2��0����B��2m+1��0������A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪP���Գ���Ϊl��x=1��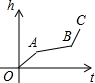 ���ٵ���һ��������עˮ����������ע������עˮ�����У�ˮ��߶�h��ʱ��t�ı仯������ͼ��ʾ��ͼ��OABCΪһ���ߣ��������������״����ͼ�еģ�������
���ٵ���һ��������עˮ����������ע������עˮ�����У�ˮ��߶�h��ʱ��t�ı仯������ͼ��ʾ��ͼ��OABCΪһ���ߣ��������������״����ͼ�еģ�������