题目内容
10.某学校初三年级男生共200名,随机抽取10名测量他们的身高(单位:cm)为:181,176,169,155,163,175,173,167,165,166.
(1)求这10名男生的平均身高和上面这组数据的中位数;
(2)估计该校初三年级男生身高高于170cm的人数;
(3)从身高为181,176,175,173的男生中任选2名,求身高为181cm的男生被抽中的概率.
分析 (1)利用平均数及中位数的定义分别计算后即可确定正确的结论;
(2)用样本平均数估计总体平均数即可;
(3)列表将所有等可能的结果列举出来,利用概率公式求解即可.
解答 解:(1)平均身高为:$\frac{181+176+169+155+163+175+17167+165+166}{10}$=169cm;
∵排序后位于中间的两数167和169,
∴中位数为168cm;
(2)∵10人中身高高于170的有4人,
∴200名初三学生中共有200×$\frac{4}{10}$=80人;
(3)身高分别为181,176,175,173的四名男生分别用1,2,3,4表示,
列表得:
| 1 | 2 | 3 | 4 | |
| 1 | 12 | 13 | 14 | |
| 2 | 21 | 23 | 24 | |
| 3 | 31 | 32 | 34 | |
| 4 | 41 | 42 | 43 |
∴身高为181cm的男生被抽中的概率$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查了中位数、平均数及列表与树状图的知识,解题的关键是能够利用列表将所有等可能的结果列举出来,难度不大.

练习册系列答案
相关题目
5.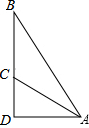 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )| A. | 5米 | B. | 6米 | C. | 8米 | D. | (3+$\sqrt{5}$)米 |
15.如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y=x2+1,则原抛物线的解析式不可能的是( )
| A. | y=x2-1 | B. | y=x2+6x+5 | C. | y=x2+4x+4 | D. | y=x2+8x+17 |
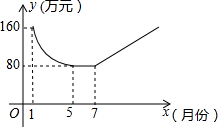 保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.
保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示. 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.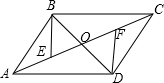 如图,?ABCD的对角线AC、BD相交于点O,AE=CF.
如图,?ABCD的对角线AC、BD相交于点O,AE=CF.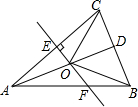 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )