题目内容
13.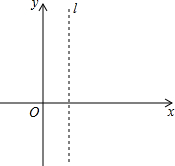 已知抛物线y=-x2+bx+c与x轴交于点A(m-2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
已知抛物线y=-x2+bx+c与x轴交于点A(m-2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.(1)求抛物线解析式.
(2)直线y=kx+2(k≠0)与抛物线相交于两点M(x1,y1),N(x2,y2)(x1<x2),当|x1-x2|最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.
分析 (1)根据对称轴公式求出b的值,再根据根与系数的关系求出c的值,从而求出二次函数解析式;
(2)将一次函数与二次函数组成方程组,得到一元二次方程x2+(k-2)x-1=0,根据根与系数的关系求出k的值,进而求出M(-1,0),N(1,4);
(3)O,B,P,C构成多边形的周长L=OB+BP+PC+CO,根据线段OB平移过程中,OB、PC长度不变,得到要使L最小,只需BP+CO最短,作点P关于x轴(或OB)对称点P′(1,-4),
连接C′P′与x轴交于点B′,然后根据平移知识和勾股定理解答.
解答 解:(1)由已知对称轴为x=1,得-$\frac{b}{2×(-1)}$=1,
∴b=2,
抛物线y=-x2+bx+c与x轴交于点A(m-2,0)和B(2m+1,0),
即-x2+2x+c=0的解为m-2和2m+1,
(m-2)+(2m+1)=2,
3m=3,
m=1,
将m=1代入(m-2)(2m+1)=-c得,
(1-2)(2+1)=-c,
∴c=3,
∴m=1,c=3,
抛物线的解析式为y=-x2+2x+3;
(2)由$\left\{\begin{array}{l}y=kx+2\\ y=-{x}^{2}+2x+3\end{array}\right.$,
∴x2+(k-2)x-1=0,
x1+x2=-(k-2),x1x2=-1,
∴(x1-x2)2=(x1+x2)2-4x1x2=(k-2)2+4,
∴当k=2时,(x1-x2)2的最小值为4,即|x1-x2|的最小值为2,
∴x2-1=0,由x1<x2可得x1=-1,x2=1,即y1=4,y2=0,
∴当|x1-x2|最小时,抛物线与直线的交点为M(-1,0),N(1,4);
(3)O(0,0),B(3,0),P(1,4),C(0,3),
O,B,P,C构成多边形的周长L=OB+BP+PC+CO,
∵线段OB平移过程中,OB、PC长度不变,
∴要使L最小,只需BP+CO最短,
如图,平移线段OC到BC′,四边形OBC′C是矩形,
∴C′(3,3),
作点P关于x轴(或OB)对称点P′(1,-4),
连接C′P′与x轴交于点B′,
设C′P′解析式为y=ax+n,
∴$\left\{\begin{array}{l}a+n=-4\\ 3a+n=3\end{array}\right.$,解得$\left\{\begin{array}{l}a=\frac{7}{2}\\ n=-\frac{15}{2}\end{array}\right.$,
∴y=$\frac{7}{2}$x-$\frac{15}{2}$,
当y=0时,x=$\frac{15}{7}$,
∴B′($\frac{15}{7}$,0),
又3-$\frac{15}{7}$=$\frac{6}{7}$,
故点B向左平移$\frac{6}{7}$,平移到B′,
同时,点O向左平移$\frac{6}{7}$,平移到0′(-$\frac{6}{7}$,0).
即线段OB向左平移$\frac{6}{7}$时,周长L最短,
此时,线段BP,CO之和最短为P′C′=$\sqrt{{7}^{2}+{2}^{2}}$=$\sqrt{53}$,O′B′=OB=3,CP=$\sqrt{2}$,
∴当线段OB向左平移$\frac{6}{7}$,即点O平移到O′(-$\frac{6}{7}$,0),点B平移到B′($\frac{15}{7}$,0)时,周长L最短为$\sqrt{53}$+$\sqrt{2}$+3.
点评 本题考查了二次函数综合题,涉及待定系数法求二次函数解析式、函数与方程的关系、最短路径问题等,综合性强,值得关注.

| A. | 3cm | B. | 4cm | C. | 9cm | D. | 10cm |
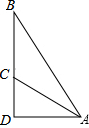 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )| A. | 5米 | B. | 6米 | C. | 8米 | D. | (3+$\sqrt{5}$)米 |
| A. | 20% | B. | 40% | C. | -220% | D. | 30% |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
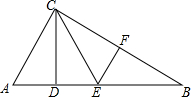 如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF.
如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF. 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点. (1)已知m是方程x2-x-1=0的一个根,求m(m+1)2-m2(m+3)+4的值;
(1)已知m是方程x2-x-1=0的一个根,求m(m+1)2-m2(m+3)+4的值;