题目内容
6. 设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
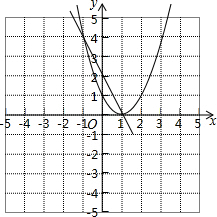
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
分析 (1)把k=0代入函数解析式即可得到所求的函数解析式,根据函数解析式作出图象;
(2)根据函数图象回答问题;
(3)由“左加右减,上加下减”的规律写出函数解析式,根据函数图象的增减性来求函数y3的最小值.
解答 解:(1)当k=0时,y=-(x-1)(x+3),所画函数图象如图所示: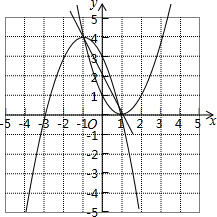
(2)①k取0和2时的函数图象关于点(0,2)中心对称.
②函数y=(x-1)[(k-1)x+(k-3)](k是常数)的图象都经过(1,0)和(-1,4).
(3)由题意可得y2=(x-1)[(2-1)x+(2-3)]=(x-1)2,
平移后的函数y3的表达式为y3=(x-1+4)2-2=(x+3)2-2.
所以当x=-3时,函数y3的最小值是-2.
点评 本题考查了抛物线与x轴的交点坐标,二次函数图象,二次函数图象与几何变换以及二次函数的最值.熟练掌握函数图象的性质和学会读图是解题的关键.

练习册系列答案
相关题目
17.近年来,国家大力提倡大学生创业,2015年小王就要毕业了,因为他学的是市场营销专业,所以毕业后想开一个商店,经过市场调研发现,若投资一个面积为x(单位:m2)的商铺,所需购买费用(单位:万元)与x+2成正比例,装修费用(单位:万元)与x2成正比例,并在调查过程中得到了表格中的数据:
(1)如果小王用从银行贷款30万元、父亲资助20万元、自己大学期间勤工俭学的收入1.6万元,共51.6万元投资一个商铺,请计算小王投资的这个商铺的面积为多少平方米;(总费用=购买费用+装修费用)
(2)购买商铺后,小王准备经营童鞋专卖店,已知专卖店代理的某品牌童鞋的进价为每双40元,该品牌童鞋日销售量y(双)与销售单价x(元/双)之间的关系式为:
y=$\left\{\begin{array}{l}{-2x+140(40≤x≤58)}\\{-x+82(58<x≤71)}\end{array}\right.$
①求他的销售利润w(元)与销售单价x(元/双)之间的函数关系式.
②小王每月需向银行还贷2075元,另童鞋店每月需缴纳水电费、营业税等固定费用3000元,通过计算判断,小王每月(按30天计算)能否有盈余?如果有,最多盈余多少元?(盈余=销售利润-固定费用-银行贷款)
| 商铺的面积(m2) | 购买费用(万元) | 装修费用(万元) |
| 1 | 1.8 | 0.3 |
(2)购买商铺后,小王准备经营童鞋专卖店,已知专卖店代理的某品牌童鞋的进价为每双40元,该品牌童鞋日销售量y(双)与销售单价x(元/双)之间的关系式为:
y=$\left\{\begin{array}{l}{-2x+140(40≤x≤58)}\\{-x+82(58<x≤71)}\end{array}\right.$
①求他的销售利润w(元)与销售单价x(元/双)之间的函数关系式.
②小王每月需向银行还贷2075元,另童鞋店每月需缴纳水电费、营业税等固定费用3000元,通过计算判断,小王每月(按30天计算)能否有盈余?如果有,最多盈余多少元?(盈余=销售利润-固定费用-银行贷款)
15.如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y=x2+1,则原抛物线的解析式不可能的是( )
| A. | y=x2-1 | B. | y=x2+6x+5 | C. | y=x2+4x+4 | D. | y=x2+8x+17 |
 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.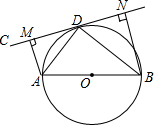 如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.
如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.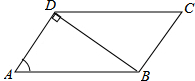 如图,在?ABCD中,连接BD,AD⊥BD,AB=4,sinA=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,AD⊥BD,AB=4,sinA=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.