题目内容
2.已知x-$\frac{1}{x}$=4,求$\frac{{x}^{2}}{{x}^{4}-5{x}^{2}+1}$的值.分析 将x-$\frac{1}{x}$=4两边平方,然后将所求的式子分子分母同乘以x2后即可求出答案.
解答 解:∵x-$\frac{1}{x}$=4,
∴(x-$\frac{1}{x}$)2=16,
∴x2-2+$\frac{1}{{x}^{2}}$=16,
∴x2+$\frac{1}{{x}^{2}}$=18,
∴原式=$\frac{1}{{x}^{2}-5+\frac{1}{{x}^{2}}}$
=$\frac{1}{18-5}$
=$\frac{1}{13}$
点评 本题考查分式的运算,解题的关键是求出x2+$\frac{1}{{x}^{2}}$=18,本题属于中等题型.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
17.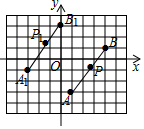 如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
 如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )| A. | (a-4,b+2) | B. | (a-4,b-2) | C. | (a+4,b+2) | D. | (a+4,b-2) |
7.三角形的外心到三角形三个顶点的距离相等,它是三角形( )
| A. | 三个内角平分线的交点 | B. | 三边垂直平分线的交点 | ||
| C. | 三条高线的交点 | D. | 三条中线的交点 |
20.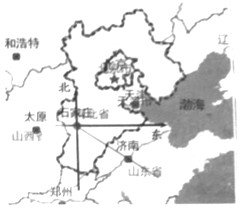 如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
 如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )| A. | 北偏西56°方向上 | B. | 北偏西34°方向上 | C. | 南偏西34°方向上 | D. | 南偏东56°方向上 |
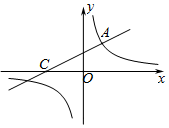 如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.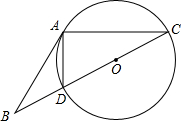 如图,△ABC中,O为BC上一点,⊙O过A,C两点交BC于D,BA为⊙O的切线,若sin∠B=$\frac{3}{5}$,求tan∠BAD的值.
如图,△ABC中,O为BC上一点,⊙O过A,C两点交BC于D,BA为⊙O的切线,若sin∠B=$\frac{3}{5}$,求tan∠BAD的值.