题目内容
16.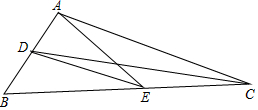 如图所示,在△ABC中,∠BAC=100°,∠ACB=30°,∠EAC=20°,CD平分∠ACB,则∠DEB的度数是25°.
如图所示,在△ABC中,∠BAC=100°,∠ACB=30°,∠EAC=20°,CD平分∠ACB,则∠DEB的度数是25°.
分析 过D做DG⊥AC交CA的延长线于G,做DH⊥BC交BC于H,做DF⊥AE交AE于F点,根据角平分线的性质可得出DG=DH,通过角的计算可得出∠GAD=∠FAD,结合∠DGA=∠DFA=90°及DA=DA,即可证出△ADG≌△ADF(AAS),根据全等三角形的性质可得出DG=DF,从而得出DF=FH及DE平分∠AEB,根据角平分线的定义结合三角形外角的性质即可求出∠DEB的度数.
解答 解:过D做DG⊥AC交CA的延长线于G,做DH⊥BC交BC于H,做DF⊥AE交AE于F点,如图所示.
∵CD平分∠ACB,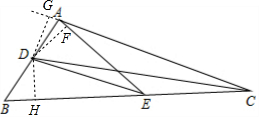
∴DG=DH.
∵∠BAC=100°,∠EAC=20°,
∴∠GAD=180°-∠BAC=80°,∠FAD=∠BAC-∠EAC=80°,
∴∠GAD=∠FAD.
在△ADG和△ADF中,$\left\{\begin{array}{l}{∠GAD=∠FAD}\\{∠DGA=∠DFA=90°}\\{DA=DA}\end{array}\right.$,
∴△ADG≌△ADF(AAS),
∴DG=DF.
∵DG=DH,
∴DF=FH,
∴DE平分∠AEB.
∴∠DEB=$\frac{1}{2}$∠AEB=$\frac{1}{2}$(∠EAC+∠ACB)=25°.
故答案为:25°.
点评 本题考查了全等三角形的判定与性质、角平分线的性质以及三角形外角的性质,通过证△ADG≌△ADF找出DG=DH是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
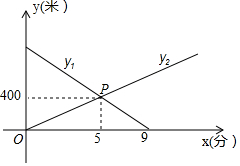 甲从A地出发匀速走向B地,同时乙从B地出发按同一路线匀速走向A地,如图所示,y1、y2分别表示甲、乙离B地的距离(米)与行走时间x(分)之间的关系.
甲从A地出发匀速走向B地,同时乙从B地出发按同一路线匀速走向A地,如图所示,y1、y2分别表示甲、乙离B地的距离(米)与行走时间x(分)之间的关系. 如图,P是△ABC两个外角∠DBC与∠ECB平分线的交点,∠A=80°,则∠BPC=50°.
如图,P是△ABC两个外角∠DBC与∠ECB平分线的交点,∠A=80°,则∠BPC=50°.