题目内容
17.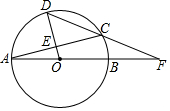 如图,AB是⊙O的直径,D是$\widehat{AC}$上一点,且OD经过AC的中点E,连接DC并延长交AB的延长线于点F.
如图,AB是⊙O的直径,D是$\widehat{AC}$上一点,且OD经过AC的中点E,连接DC并延长交AB的延长线于点F.(1)当∠A=16°,求∠F的大小;
(2)当⊙O的半径为6,DE=4,求CD的长.
分析 (1)连接OC,由垂径定理得出OD⊥AC,$\widehat{AD}=\widehat{CD}$,得出∠AOE=∠COE,求出∠AOE=∠COE=74°,由圆周角定理得出∠DCE=$\frac{1}{2}$∠AOE=37°,再由三角形的外角性质即可得出结果;
(2)求出OE=OD-DE=2,在Rt△OCE中,由勾股定理求出CE=4$\sqrt{2}$,在Rt△DCE中,由勾股定理求出CD即可.
解答 解:(1)如图,连接OC,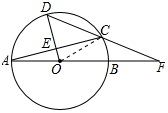
∵E是AC的中点,
∴AE=CE,
∴OD⊥AC,$\widehat{AD}=\widehat{CD}$,
∴∠AOE=∠COE,
∵∠BAC=16°,
∴∠AOE=∠COE=74°,
∴∠DCE=$\frac{1}{2}$∠AOE=37°,
∴∠F=∠DCE-∠BAC=37°-16°=21°;
(2)∵OC=OD=6,DE=4,
∴OE=OD-DE=2,
在Rt△OCE中,由勾股定理得:CE=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$,
在Rt△DCE中,由勾股定理得:CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=4$\sqrt{3}$.
点评 本题考查了垂径定理、圆周角定理、勾股定理、直角三角形的性质以及三角形的外角性质等知识;熟练掌握圆周角定理和勾股定理是解决问题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5.如果点(a,b)在直线y=-x+1上,二次函数y=ax2+bx的图象必经过( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
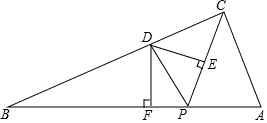 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=10,点P是边AB上任意一点,连接PC,∠CPB的平分线交BC于点D,过点D分别作PC、PB的垂线,垂足分别为点E、F,当△CED与△BDF相似时,AP的长为$\frac{5\sqrt{5}}{2}$或$\sqrt{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=10,点P是边AB上任意一点,连接PC,∠CPB的平分线交BC于点D,过点D分别作PC、PB的垂线,垂足分别为点E、F,当△CED与△BDF相似时,AP的长为$\frac{5\sqrt{5}}{2}$或$\sqrt{5}$.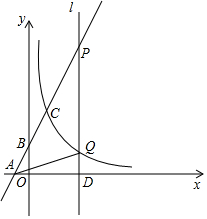 如图,在平面直角坐标系中,一次函数y=2x+2与x轴y轴分别交于点A,B与反比例函数y=$\frac{4}{x}$在第一象限交于点C.
如图,在平面直角坐标系中,一次函数y=2x+2与x轴y轴分别交于点A,B与反比例函数y=$\frac{4}{x}$在第一象限交于点C.
 如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F
如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F