Question

9．如图，△AOB是等腰三角形，顶点A的坐标为（2，$\sqrt{5}$），底边OB在x轴上，将△AOB绕点B按顺时针方向旋转一定的角度后的△A'O'B'，点A的对应点A'在x轴上，则点O'的坐标为（　　）

• A． （$\frac{20}{3}$，$\frac{10}{3}$）
• B． （$\frac{16}{3}$，$\frac{{4\sqrt{5}}}{3}$）
• C． （$\frac{20}{3}$，$\frac{{4\sqrt{5}}}{3}$）
• D． （$\frac{16}{3}$，$4\sqrt{3}$）

Answer 1

分析 过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，根据点A的坐标求出OC、AC，再利用勾股定理列式计算求出OA，根据等腰三角形三线合一的性质求出OB，根据旋转的性质可得BO′=OB，∠A′BO′=∠ABO，然后解直角三角形求出O′D、BD，再求出OD，然后写出点O′的坐标即可．

解答 解：如图，过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，
∵A（2，$\sqrt{5}$），
∴OC=2，AC=$\sqrt{5}$，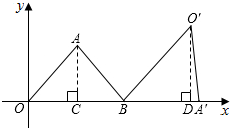
由勾股定理得，OA=$\sqrt{{OC}^{2}{+AC}^{2}}$=$\sqrt{{2}^{2}{+（\sqrt{5}）}^{2}}$=3，
∵△AOB为等腰三角形，OB是底边，
∴OB=2OC=2×2=4，
由旋转的性质得，BO′=OB=4，∠A′BO′=∠ABO，
∴O′D=4×$\frac{\sqrt{5}}{3}$=$\frac{4\sqrt{5}}{3}$，
BD=4×$\frac{2}{3}$=$\frac{8}{3}$，
∴OD=OB+BD=4+$\frac{8}{3}$=$\frac{20}{3}$，
∴点O′的坐标为（$\frac{20}{3}$，$\frac{4\sqrt{5}}{3}$），
故选：C．

点评 本题考查了坐标与图形变化-旋转，主要利用了勾股定理，等腰三角形的性质，解直角三角形，熟记性质并作辅助线构造出直角三角形是解题的关键．