题目内容
 如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.
如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.(1)如果EF=8,BC=12,求AD和GH的长;
(2)如果AD=4,BC=10,求EF和GH的长.
考点:梯形中位线定理,平行线分线段成比例
专题:
分析:(1)延长BA、CD,交于点P,根据平行线分线段成比例得出AD∥EF∥GH∥BC,于是四边形BCFE、ADHG都是梯形.由GH是梯形BCFE的中位线,根据梯形中位线定理可得GH=
(EF+BC)=10;又EF是梯形ADHG的中位线,根据梯形中位线定理可求出AD的长;
(2)过点A作AS∥CD分别交EF、GH、BC于点P、Q、S,就看得出四边形ADCS,ADFP,PFQH,QHCS是平行四边形,就有AD=PF=QH=CS=4,得出BS=6,再由△AE∽△ABS和△AGQ∽△ABS,由相似三角形的性质就可以求出EP,GQ的值,从而EF和GH的长.
| 1 |
| 2 |
(2)过点A作AS∥CD分别交EF、GH、BC于点P、Q、S,就看得出四边形ADCS,ADFP,PFQH,QHCS是平行四边形,就有AD=PF=QH=CS=4,得出BS=6,再由△AE∽△ABS和△AGQ∽△ABS,由相似三角形的性质就可以求出EP,GQ的值,从而EF和GH的长.
解答: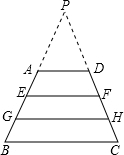 解:(1)如图,延长BA、CD,交于点P.
解:(1)如图,延长BA、CD,交于点P.
∵AD∥BC,
∴
=
,
∵AE=EG=GB,DF=FH=HC,
∴
=
,
∴
=
,
∴EF∥AD,
同理GH∥AD,
∵AD∥BC,
∴AD∥EF∥GH∥BC,
∴四边形BCFE、ADHG都是梯形.
在梯形BCFE中,∵EG=GB,FH=HC,
∴GH是梯形BCFE的中位线,
∴GH=
(EF+BC)=
(8+12)=10;
在梯形ADHG中,∵AE=EG,DF=FH,
∴EF是梯形ADHG的中位线,
∴EF=
(AD+GH),
∴AD=2EF-GH=2×8-10=6;
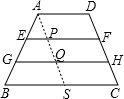
(2)过点A作AS∥CD分别交EF、GH、BC于点P、Q、S,
∵AD∥EF∥GH∥BC,
∴四边形ADCS,ADFP,PFQH,QHCS是平行四边形,
∴AD=PF=QH=CS=4,
∴BS=6.
∵EF∥BC,
∴△AEP∽△ABS,
∴
=
,
∵AE=EG=BG,设AE=EG=BG=a,
∴AE=a,AG=2a,AB=3a.
∴
=
,
∴
=
,
∴EP=2,
∴EF=6.
∵GH∥BC,
∴△AGQ∽△ABS,
∴
=
,
∴
=
,
∴GQ=4,
∴GH=8.
 解:(1)如图,延长BA、CD,交于点P.
解:(1)如图,延长BA、CD,交于点P.∵AD∥BC,
∴
| PA |
| AB |
| PD |
| DC |
∵AE=EG=GB,DF=FH=HC,
∴
| PA |
| 3AE |
| PD |
| 3DF |
∴
| PA |
| AE |
| PD |
| DF |
∴EF∥AD,
同理GH∥AD,
∵AD∥BC,
∴AD∥EF∥GH∥BC,
∴四边形BCFE、ADHG都是梯形.
在梯形BCFE中,∵EG=GB,FH=HC,
∴GH是梯形BCFE的中位线,
∴GH=
| 1 |
| 2 |
| 1 |
| 2 |
在梯形ADHG中,∵AE=EG,DF=FH,
∴EF是梯形ADHG的中位线,
∴EF=
| 1 |
| 2 |
∴AD=2EF-GH=2×8-10=6;
(2)过点A作AS∥CD分别交EF、GH、BC于点P、Q、S,
∵AD∥EF∥GH∥BC,
∴四边形ADCS,ADFP,PFQH,QHCS是平行四边形,
∴AD=PF=QH=CS=4,
∴BS=6.
∵EF∥BC,
∴△AEP∽△ABS,
∴
| AE |
| AB |
| EP |
| BS |

∵AE=EG=BG,设AE=EG=BG=a,
∴AE=a,AG=2a,AB=3a.
∴
| AE |
| AB |
| 1 |
| 3 |
∴
| 1 |
| 3 |
| EP |
| 6 |
∴EP=2,
∴EF=6.
∵GH∥BC,
∴△AGQ∽△ABS,
∴
| AG |
| AB |
| GQ |
| BS |
∴
| 2a |
| 3a |
| GQ |
| 6 |
∴GQ=4,
∴GH=8.
点评:本题考查了梯形中位线定理,平行线分线段成比例定理,平行四边形、相似三角形的判定与性质,准确作出辅助线是解题的关键.

练习册系列答案
相关题目
 如图,BD、CE为△ABC的中线,BD与CE交于点G,则BG:GD=
如图,BD、CE为△ABC的中线,BD与CE交于点G,则BG:GD= 如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴,y轴分别交于A,B两点,点A的坐标为(4,0),OC与⊙D相交于点C,∠OCA=30°.
如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴,y轴分别交于A,B两点,点A的坐标为(4,0),OC与⊙D相交于点C,∠OCA=30°.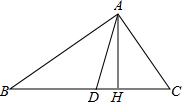 如图,在△ABC中,∠ACB=90°,CD为∠ACB的角平分线,CH⊥AB于H,若AD=p,BD=q,求CH的长.
如图,在△ABC中,∠ACB=90°,CD为∠ACB的角平分线,CH⊥AB于H,若AD=p,BD=q,求CH的长.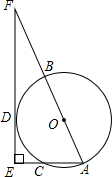 如图,AB是⊙O的直径,AC为弦,D是
如图,AB是⊙O的直径,AC为弦,D是