题目内容
 如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴,y轴分别交于A,B两点,点A的坐标为(4,0),OC与⊙D相交于点C,∠OCA=30°.
如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴,y轴分别交于A,B两点,点A的坐标为(4,0),OC与⊙D相交于点C,∠OCA=30°.(1)求OB的长;
(2)⊙D经过怎样平移,使得⊙D与y轴相切?(写出一种平移方法即可)
(3)求阴影部分面积和.
考点:圆的综合题
专题:
分析:(1)连接AB,由圆周角定理可得∠OBA的度数,解直角三角形BOA,即可求出OB的长;
(2)过D作DM⊥OB,利用已知条件可求出DM的长,则⊙D向右平移OD-DM即可使得⊙D与y轴相切;
(3)利用两个扇形的面积-两个三角形的面积即可得到阴影部分面积和.
(2)过D作DM⊥OB,利用已知条件可求出DM的长,则⊙D向右平移OD-DM即可使得⊙D与y轴相切;
(3)利用两个扇形的面积-两个三角形的面积即可得到阴影部分面积和.
解答: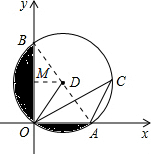 解:(1)连接AB,
解:(1)连接AB,
∵∠OCA=30°,
∴∠OBA=∠0CA=30°,
∵AO⊥BO,
∴∠BOA=90°,
∵点A的坐标为(4,0),
∴OA=4,
∴OB=4
;
(2)过D作DM⊥OB,
∵∠BOA=90°,
∴AB为圆的直径,
∵∠OBA=30°,OA=4,
∴AB=8,
∴BD=4,
∴DM=2,
∴⊙D向右平移OD-DM=2,即可使得⊙D与y轴相切;
(3)∵S扇形BDO=
=
=
,S△BDO=
DM•BO=
×2×4
=4
,S扇形ODA=
=
=
,S△ODA=
×4×2
=4
,
∴阴影部分面积和=
+
-4
-4
=8π-8
.
 解:(1)连接AB,
解:(1)连接AB,∵∠OCA=30°,
∴∠OBA=∠0CA=30°,
∵AO⊥BO,
∴∠BOA=90°,
∵点A的坐标为(4,0),
∴OA=4,
∴OB=4
| 3 |
(2)过D作DM⊥OB,
∵∠BOA=90°,
∴AB为圆的直径,
∵∠OBA=30°,OA=4,
∴AB=8,
∴BD=4,
∴DM=2,
∴⊙D向右平移OD-DM=2,即可使得⊙D与y轴相切;
(3)∵S扇形BDO=
| nπr2 |
| 360 |
| 120×π×16 |
| 360 |
| 16π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| nπr2 |
| 360 |
| 60×π×16 |
| 360 |
| 8π |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∴阴影部分面积和=
| 16π |
| 3 |
| 8π |
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了和圆有关的综合题目,用到的知识点有圆周角定理、平移的性质、解直角三角形的有关知识、特殊角的三角函数值、扇形面积公式运用以及三角形面积公式运用,题目的综合性较强,难度中等.

练习册系列答案
相关题目
下列事件中,是必然事件的是( )
| A、打开电视机,正在播放新闻 |
| B、在同一年出生的367名学生中,至少有两人的生日是同一天 |
| C、通过长期努力学习,你会成为数学家 |
| D、下雨天,每个人都打着雨伞 |
 下列形状的纸片,经过折叠可以围成一个棱柱的是
下列形状的纸片,经过折叠可以围成一个棱柱的是 如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.
如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.