题目内容
一次函数y=ax+b与二次函数y=ax2+bx在同一坐标系中的图象大致为( )
A、 |
B、 |
C、 |
D、 |
考点:二次函数的图象,一次函数的图象
专题:数形结合
分析:对于每个选项,先根据二次函数的图象确定a和b的符号,然后根据一次函数的性质看一次函数图象的位置是否正确,若正确,说明它们可在同一坐标系内存在.
解答:解:A、由二次函数y=ax2+bx的图象得a>0,b<0,则一次函数y=ax+b经过第一、三、四象限,且它们的交点为(1,0),所以A选项正确;
B、由二次函数y=ax2+bx的图象得a>0,b>0,则一次函数y=ax+b经过第一、二、三象限,所以B选项错误;
C、由二次函数y=ax2+bx的图象得a<0,b>0,则一次函数y=ax+b经过第一、二、四象限,所以C选项错误;
D、由二次函数y=ax2+bx的图象得a<0,b<0,则一次函数y=ax+b经过第二、三、四象限,所以D选项错误.
故选A.
B、由二次函数y=ax2+bx的图象得a>0,b>0,则一次函数y=ax+b经过第一、二、三象限,所以B选项错误;
C、由二次函数y=ax2+bx的图象得a<0,b>0,则一次函数y=ax+b经过第一、二、四象限,所以C选项错误;
D、由二次函数y=ax2+bx的图象得a<0,b<0,则一次函数y=ax+b经过第二、三、四象限,所以D选项错误.
故选A.
点评:本题考查了二次函数的图象:二次函数的图象为抛物线,可能利用列表、描点、连线画二次函数的图象.也考查了二次函数图象与系数的关系.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
一个二次函数的图象的顶点坐标是(2,4),且过另一点(0,-4),则这个二次函数的解析式为( )
| A、y=-2(x+2)2+4 |
| B、y=-2(x-2)2+4 |
| C、y=2(x+2)2-4 |
| D、y=2(x-2)2-4 |
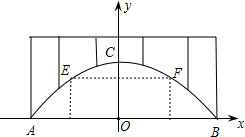 廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图,以水面AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)
廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图,以水面AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)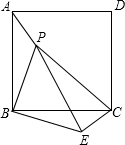 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBE重合,若PB=3,则PE=
如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBE重合,若PB=3,则PE=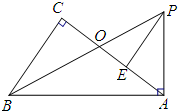 如图,在△ABC中,∠C=90°,△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
如图,在△ABC中,∠C=90°,△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.