题目内容
如图，AB=AD，∠BAD=∠CAE，AC=AE，求证：BC=DE．考点：全等三角形的判定与性质
专题：证明题
分析：由条件可得到∠BAC=∠DAE，从而可证明△ABC≌△ADE，可得出BD=DE．
解答：证明：∵∠BAD=∠CAE，
∴∠BAD+∠DAC=∠CAE+∠DAC，
即∠BAC=∠DAE，
在△ABC和△ADE中
∴△ABC≌△ADE（SAS），
∴BC=DE．
∴∠BAD+∠DAC=∠CAE+∠DAC，
即∠BAC=∠DAE，
在△ABC和△ADE中
|
∴△ABC≌△ADE（SAS），
∴BC=DE．
点评：本题主要考查全等三角形的判定和性质，由条件得到∠BAC=∠DAE是解题的关键．
练习册系列答案
相关题目
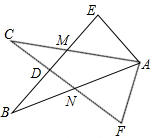如图，在Rt△AEB和Rt△AFC中，BE与AC相交于点M，与CF相交于点D，AB与CF相交于N，∠E=∠F=90°，∠EAC=∠FAB，AE=AF．给出下列结论：①∠B=∠C；②CD=DN；③BE=CF；④△ACN≌△ABM．其中正确的结论是
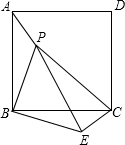如图，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转与△CBE重合，若PB=3，则PE=