题目内容
2．若x2+y2+2x-6y+10=0，x、y均为有理数，则xy的值为-3．分析 先将x2+y2+2x-6y+10=0，整理成平方和的形式，再根据非负数的性质可求出x、y的值，进而可求出xy的值．
解答 解：由题意得：x2+y2+2x-6y+10=（x+1）2+（y-3）2=0，
由非负数的性质得x=-1，y=3．
则xy=-1×3=-3．
故答案为-3．
点评 本题考查了配方法的应用，初中阶段有三种类型的非负数：（1）绝对值；（2）偶次方；（3）二次根式（算术平方根）．当它们相加和为0时，必须满足其中的每一项都等于0．根据这个结论可以求解这类题目．
练习册系列答案
相关题目
如图，小明要测量河内小岛B到河边公路AD的距离，在点A处测得∠BAD=37°，沿AD方向前进150米到达点C，测得∠BCD=45°．求小岛B到河边公路AD的距离．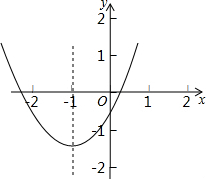
已知抛物线y=ax2+bx+c（a＞0）的对称轴为直线x=-1，该抛物线与x轴的一个交点为（x1，0），且0＜x1＜1，有下列结论：①abc＞0；②9a-3b+c＞0；③b＜a；④3a+c＞0．其中正确结论的个数是（ ）