题目内容
7. 超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.
超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.(1)求B、C两点间的距离.
(2)请判断此车是否超过了BC路段限速40千米/小时的速度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 (1)根据BC=AC•tan60°直接代入计算即可,
(2)根据此车从B处到C处所用的时间为5秒可得出小车在BC路段的速度为30$\sqrt{3}$÷$\frac{5}{3600}$,再与40比较即可.
解答 解:(1)∵AC=30米,∠BAC=60°,
∴在Rt△ABC中,BC=AC•tan60°=30$\sqrt{3}$(米),
(2)∵此车从B处到C处所用的时间为5秒,
∴小车在BC路段的速度为30$\sqrt{3}$÷$\frac{5}{3600}$≈37.4(千米/小时)
∵37.4<40
∴此车在BC路段没有超速.
点评 此题考查了解直角三角形的应用,用到的知识点是特殊角的三角函数值、三角函数,关键是根据已知条件求出BC的长.

练习册系列答案
相关题目
17. 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )
如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )
 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )
如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )| A. | 只有①③ | B. | 只有①③④ | C. | 只有②④ | D. | ①②③④ |
2.计算$\frac{x-1}{x}$+$\frac{1}{x}$=( )
| A. | 1 | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x}$ | D. | $\frac{x-1}{x}$ |
12.计算($\frac{3}{2}$)-2的结果是( )
| A. | $\frac{4}{9}$ | B. | $\frac{9}{4}$ | C. | -$\frac{9}{4}$ | D. | 0 |
16.下列计算正确的是( )
| A. | (a4)2=a6 | B. | a+2a=3a2 | C. | a7÷a2=a5 | D. | a(a2+a+1)=a3+a2 |
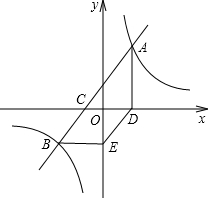 如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.
如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由. 如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC外接圆的半径为$\sqrt{3}$cm.
如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC外接圆的半径为$\sqrt{3}$cm.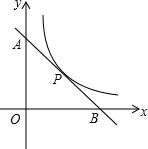 如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )
如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )