题目内容
4.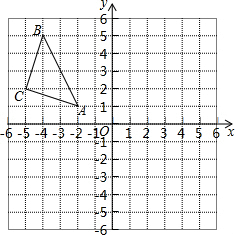 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).△ABC关于直线 l:x=-1对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1;
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).△ABC关于直线 l:x=-1对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1;(1)请在图中画出△A1B1C1,并写出点的坐标:A1(0,1)、B1(3,2)、C1(2,5).
(2)计算△A1B1C1的面积为5.
分析 (1)根据轴对称的性质画出△A1B1C1,并写出各点坐标即可;
(2)先判断出△A1B1C1的形状,再求出其面积即可.
解答 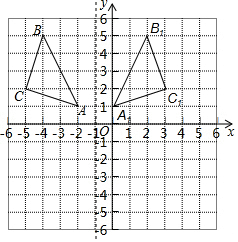 解:(1)如图,△A1B1C1即为所求,A1(0,1)、B1(3,2)、C1(2,5).
解:(1)如图,△A1B1C1即为所求,A1(0,1)、B1(3,2)、C1(2,5).
故答案为:0,1;3,2;2,5;
(2)∵A1B12=42+22=20,A1C12=32+12=10,
B1C12=32+12=10,
∴A1B12=+A1C12+B1C12,
∴△A1B1C1是等腰直角三角形,
∴△A1B1C1的面积=$\frac{1}{2}$×$\sqrt{10}$×$\sqrt{10}$=5.
故答案为:5.
点评 本题考查的是作图-轴对称变换及勾股定理的逆定理,熟知轴对称的性质是解答此题的关键.

练习册系列答案
相关题目
19.在平面直角坐标系中,有A(1,2),B(4,3)两点,现另取一点C(a,1),满足:AC+BC的值最小.则a的值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
9.将350000用科学记数法表示为( )
| A. | 35×104 | B. | 3.5×105 | C. | 3.5×106 | D. | 0.35×106 |
 用五个完全相同的小正方体组成如图所示的立体图形,从上面看到的图形是( )
用五个完全相同的小正方体组成如图所示的立体图形,从上面看到的图形是( )



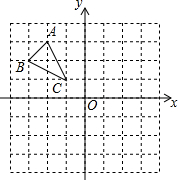 如图,已知A(-2,3),B(-3,2),C(-1,1).
如图,已知A(-2,3),B(-3,2),C(-1,1).