题目内容
5.关于x的不等式组$\left\{{\begin{array}{l}{\frac{x+21}{2}>3-x}\\{x<m}\end{array}}\right.$的所有整数解的和是-9,则m的取值范围是-2<m≤-1或1<m≤2.分析 首先确定不等式组的解集,先利用含m的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于m的不等式,从而求出m的范围.
解答 解:$\left\{\begin{array}{l}{\frac{x+21}{2}>3-x①}\\{x<m②}\end{array}\right.$
由①得x>-5;
由②得x<m;
故原不等式组的解集为-5<x<m.
又因为不等式组的所有整数解的和是-9,
所以当m<0时,这两个负整数解一定是-4和-3,由此可以得到-2<m≤-1;
当m>0时,则1<m≤2.
故m的取值范围是-2<m≤-1或1<m≤2.
点评 本题主要考查了无理数的估算,是一道较为抽象的中考题,利用数轴就能直观的理解题意,列出关于m的不等式组,临界数-1和-2的取舍是易错的地方,要借助数轴做出正确的取舍.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
20.在-2,1,0,7这四个数中,最大的数是( )
| A. | -2 | B. | 1 | C. | 0 | D. | 7 |
15.某班同学在探究弹簧的长度与外力的变化关系时,实验得到相应数据如下表:则y与x的函数图象是( )
| 砝码的质量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 |
| 弹簧的长度y(厘米) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
| A. | 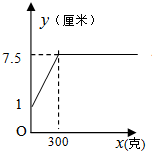 | B. | 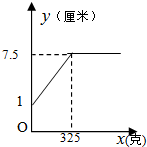 | ||
| C. | 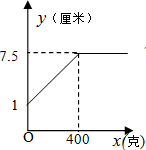 | D. | 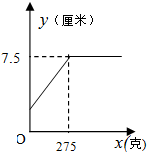 |
 如图,在△ACB中,∠ACB=90°,CD⊥AB,则以∠A为内角的三角形有△CAD,△CAB.
如图,在△ACB中,∠ACB=90°,CD⊥AB,则以∠A为内角的三角形有△CAD,△CAB.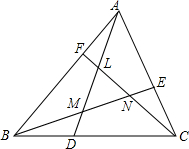 如图,D、E、F分别在△ABC的BC、CA、AB边上,$\frac{BD}{DC}$=$\frac{AF}{FB}$=$\frac{CE}{AE}$=λ,AD、BE、CF交成的三角形为LMN,求S△LMN(用S△ABC表示)
如图,D、E、F分别在△ABC的BC、CA、AB边上,$\frac{BD}{DC}$=$\frac{AF}{FB}$=$\frac{CE}{AE}$=λ,AD、BE、CF交成的三角形为LMN,求S△LMN(用S△ABC表示)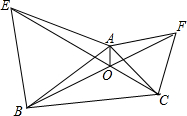 已知△ABC,分别以AB、AC、为边作等边△ABE和等边△ACF,BF与CE交于点O,连接AO,若OA=1,OC=3,OB=4,求线段CE的长.
已知△ABC,分别以AB、AC、为边作等边△ABE和等边△ACF,BF与CE交于点O,连接AO,若OA=1,OC=3,OB=4,求线段CE的长. 如图,∠ABC=∠DCB,BD、CA分别是∠ABC和∠DCB的平分线,且BD=CA.求证:OA=OD.
如图,∠ABC=∠DCB,BD、CA分别是∠ABC和∠DCB的平分线,且BD=CA.求证:OA=OD.