题目内容
10.先化简,再求值:$\frac{4x+8}{{x}^{2}-4}$÷($\frac{{x}^{2}}{x-2}$-x+2),其中(x+$\sqrt{2}$-1)(x-2)=0.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值,选出合适的x的值代入进行计算即可.
解答 解:原式=$\frac{4(x-2)}{(x+2)(x-2)}$÷$\frac{-x(x-2)}{x-2}$
=$\frac{4}{x+2}$•$\frac{1}{-x}$
=-$\frac{4}{x(x+2)}$,
∵(x+$\sqrt{2}$-1)(x-2)=0,
∴x=2或x=1-$\sqrt{2}$,
当x=2时,原式无意义,
当x=1-$\sqrt{2}$时,原式=-$\frac{4}{(1-\sqrt{2})(3-\sqrt{2})}$=$\frac{4(5+3\sqrt{2})}{7}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
18.任何整数的平方的末尾数字不可能是( )
| A. | 0,4,5,9 | B. | 1,4,6,9 | C. | 1,5,6,9 | D. | 2,3,7,8 |
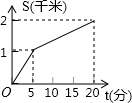
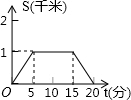
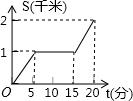
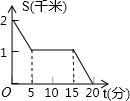
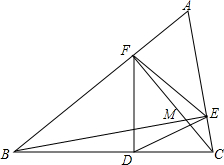 如图,△ABC,∠A=60°,BE⊥AC于点F,点D是BC中点,BE与CF相交于M
如图,△ABC,∠A=60°,BE⊥AC于点F,点D是BC中点,BE与CF相交于M 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.阴影部分的面积$\frac{1}{6}$πR2.
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.阴影部分的面积$\frac{1}{6}$πR2.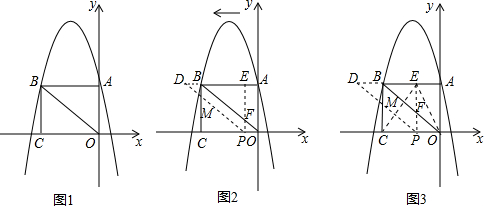
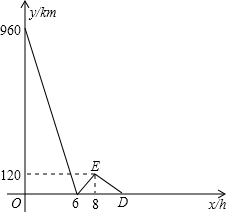 A、B两地之间的距离为960km,C地介于A、B两地之间,甲车从A地驶往C地,乙车从B地经C地驶往A地,已知两车同时出发,相向而行,结果两车同时到达C地后,甲车因故在C地须停留一段时间,然后返回A地,乙车继续驶往A地.设乙车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
A、B两地之间的距离为960km,C地介于A、B两地之间,甲车从A地驶往C地,乙车从B地经C地驶往A地,已知两车同时出发,相向而行,结果两车同时到达C地后,甲车因故在C地须停留一段时间,然后返回A地,乙车继续驶往A地.设乙车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.