题目内容
16.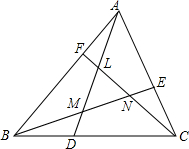 如图,D、E、F分别在△ABC的BC、CA、AB边上,$\frac{BD}{DC}$=$\frac{AF}{FB}$=$\frac{CE}{AE}$=λ,AD、BE、CF交成的三角形为LMN,求S△LMN(用S△ABC表示)
如图,D、E、F分别在△ABC的BC、CA、AB边上,$\frac{BD}{DC}$=$\frac{AF}{FB}$=$\frac{CE}{AE}$=λ,AD、BE、CF交成的三角形为LMN,求S△LMN(用S△ABC表示)
分析 作DK∥AC交BE于K,用λ表示出△ABD的面积与△ABC的面积的关系,根据平行线分线段成比例定理得到$\frac{DM}{MA}$,表示出△BMD的面积,计算即可得到答案.
解答 解: 作DK∥AC交BE于K,
作DK∥AC交BE于K,
∵$\frac{BD}{DC}$=λ,∴$\frac{BD}{BC}$=$\frac{λ}{1+λ}$,
∴△ABD的面积=$\frac{λ}{1+λ}$×△ABC的面积,
∵DK∥AC,$\frac{BD}{BC}$=$\frac{λ}{1+λ}$,
∴$\frac{DK}{EC}$=$\frac{BD}{BC}$=$\frac{λ}{1+λ}$,又$\frac{CE}{AE}$=λ,
∴$\frac{DM}{MA}$=$\frac{DK}{AE}$=$\frac{{λ}^{2}}{1+λ}$,
∴△BMD的面积=$\frac{{λ}^{2}}{1+λ+{λ}^{2}}$×△ABD的面积=$\frac{{λ}^{3}}{(1+λ+{λ}^{2})(1+λ)}$×△ABC的面积,
同理△AFL的面积=△CEN的面积=$\frac{{λ}^{3}}{(1+λ+{λ}^{2})(1+λ)}$×△ABC的面积,
∴S△LMN=(1+$\frac{3λ}{1+λ}$+$\frac{{3λ}^{3}}{(1+λ+{λ}^{2})(1+λ)}$)S△ABC.
点评 本题考查的是平行线分线段成比例定理和三角形的面积的计算,灵活运用定理、找准对应关系、掌握三角形的面积公式是解题的关键.

练习册系列答案
相关题目
11.用棋子摆出下列一组“口”字,按照这种方法摆下去,按照这种方法摆下去,则摆第n个“口”字需用棋子( )


| A. | n2枚 | B. | 4n枚 | C. | (4n+4)枚 | D. | (4n-4)枚 |
 如图,△ABC中,∠AEB=90°,则以AE为高的三角形是△ABE,△ABD,△ABC,△AED,△AEC,△ADC.
如图,△ABC中,∠AEB=90°,则以AE为高的三角形是△ABE,△ABD,△ABC,△AED,△AEC,△ADC.
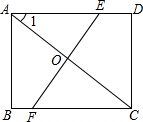 如图,是一张长4、宽3的矩形纸片,将它沿某直线折叠使A、C重合,求折痕EF的长.
如图,是一张长4、宽3的矩形纸片,将它沿某直线折叠使A、C重合,求折痕EF的长.