题目内容
14. 如图,∠ABC=∠DCB,BD、CA分别是∠ABC和∠DCB的平分线,且BD=CA.求证:OA=OD.
如图,∠ABC=∠DCB,BD、CA分别是∠ABC和∠DCB的平分线,且BD=CA.求证:OA=OD.
分析 首先根据角平分线的性质可得∠ACB=$\frac{1}{2}$∠DCB,∠DBC=$\frac{1}{2}$∠ABC,进而得到∠ACB=∠DBC,然后再根据ASA证明△ABC≌△DCB,则∠ACB=∠DBC,所以OB=OC,又BD=CA,根据等式性质可证OA=OD.
解答 证明:∵BD、CA分别是∠ABC、∠DCB的角平分线,
∴∠ACB=$\frac{1}{2}$∠DCB,∠DBC=$\frac{1}{2}$∠ABC,
∵∠ABC=∠DCB,
∴∠ACB=∠DBC,
在△ABC和△DCB中
$\left\{\begin{array}{l}{∠ABC=∠DCB}\\{CB=CB}\\{∠ACB=∠DBC}\end{array}\right.$,
∴△ABC≌△DCB(ASA),
∴∠ACB=∠DBC,
∴OB=OC,
又∵BD=CA,
∴OA=OD.
点评 本题考查三角形全等的判定与性质以及等腰三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
9. 如图,PQ∥BC,若S△APQ=3,S△PQB=6,则S△CQB等于( )
如图,PQ∥BC,若S△APQ=3,S△PQB=6,则S△CQB等于( )
 如图,PQ∥BC,若S△APQ=3,S△PQB=6,则S△CQB等于( )
如图,PQ∥BC,若S△APQ=3,S△PQB=6,则S△CQB等于( )| A. | 20 | B. | 18 | C. | 16 | D. | 9 |
 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.阴影部分的面积$\frac{1}{6}$πR2.
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.阴影部分的面积$\frac{1}{6}$πR2.
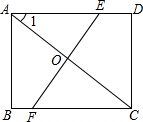 如图,是一张长4、宽3的矩形纸片,将它沿某直线折叠使A、C重合,求折痕EF的长.
如图,是一张长4、宽3的矩形纸片,将它沿某直线折叠使A、C重合,求折痕EF的长.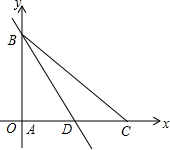 如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.
如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.