题目内容
12．在一个口袋中有4个完全相同的小球，它们的标号分别为1，2，3，4，从中随机摸出一个小球记下标号后放回，再从中随机摸出一个小球，求两次摸出的小球的标号之和大于4的概率？分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的小球的标号之和大于4的情况，再利用概率公式即可求得答案．
解答 解：画树状图得：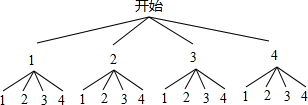
∵共有16种等可能的结果，两次摸出的小球的标号之和大于4的有10种情况，
∴两次摸出的小球的标号之和大于4的概率是：$\frac{10}{16}$=$\frac{5}{8}$．
点评 本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图，点A、O、B在同一直线上，OD平分∠AOC，OE平分∠BOC．
如图，已知正方形ABCD中，AB=12，点E在边BC上，BE=EC，将△DCE沿DE对折至△DFE，延长EF交边AB于点G，连接DG，BF．给出以下结论：
17．在Rt△ABC中，∠C=90°，∠B=30°，直角边AC的长为2cm，则斜边AB长为（ ）
| A． | $\frac{1}{2}$cm | B． | 1cm | C． | 4cm | D． | 2cm |
1．
如图，从一块直径BC是8m的圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，则圆锥的高是（ ）
如图，从一块直径BC是8m的圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，则圆锥的高是（ ）| A． | 4 | B． | 4$\sqrt{2}$ | C． | $\sqrt{15}$ | D． | $\sqrt{30}$ |