题目内容
18.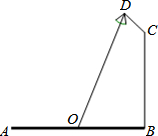 如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.
如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.
分析 延长OD,BC交于点P.解直角三角形得到DP=DC•cot30°=$\sqrt{3}$m,PC=CD÷(sin30°)=4米,通过△PDC∽△PBO,得到$\frac{PD}{PB}$代入数据即可得到结论.
解答 解:如图,延长OD,BC交于点P.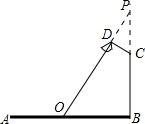
∵∠ODC=∠B=90°,∠P=30°,OB=11米,CD=2米,
∴在直角△CPD中,DP=DC•cos30°=$\sqrt{3}$m,PC=CD÷(sin30°)=4米,
∵∠P=∠P,∠PDC=∠B=90°,
∴△PDC∽△PBO,
∴$\frac{PD}{PB}=\frac{CD}{OB}$,
∴PB=$\frac{PD•OB}{CD}=\frac{2\sqrt{3}×11}{2}=11\sqrt{3}$米,
∴BC=PB-PC=(11$\sqrt{3}$-4)米.
故答案为:(11$\sqrt{3}$-4)米,
点评 本题考查了相似三角形的性质,直角三角形的性质,锐角三角函数的概念,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.暗物质粒子探测卫星“悟空”每天都将观测500万个高能粒子,传回16G数据供地面科学家团队分析研究,将500万个用科学记数法表示为( )
| A. | 5×105个 | B. | 5×106个 | C. | 5×107个 | D. | 5×108个 |
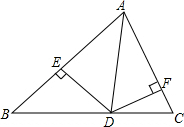 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则有下列结论:
如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则有下列结论: 抛物线y=-2x2+4x+1如图所示,作该抛物线关于点O对称的图形,得到一条新的抛物线,则新抛物线的解析式为y=2(x+12)-3.
抛物线y=-2x2+4x+1如图所示,作该抛物线关于点O对称的图形,得到一条新的抛物线,则新抛物线的解析式为y=2(x+12)-3. 如图,直线AB:y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,直线上一动点P以1cm/s的速度由点A向终点B运动,设运动时间为t(s).
如图,直线AB:y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,直线上一动点P以1cm/s的速度由点A向终点B运动,设运动时间为t(s).