题目内容
8.若关于x的一元二次方程(x-1)(x-2)=m有实数根x1、x2,且x1<x2,有下列结论:①x1=1,x2=2;
②m>-$\frac{1}{4}$;
③二次函数y=(x-1)(x-2)-m的图象对称轴为直线x=1.5;
④二次函数y=(x-1)(x-2)+m的图象与y轴交点的一定在(0,2)的上方.
其中一定正确的有②③(只填正确答案的序号).
分析 根据一元二次方程解的定义可对①进行判断;根据根的判别式对②进行判断;根据二次函数的性质可对③④进行判断.
解答 解:当m=0时,x1=1,x2=2,所以①错误;
方程整理为x2-3x+2-m=0,△=(-3)2-4(2-m)0,解得m>-$\frac{1}{4}$,所以②正确;
二次函数为y=x2-3x+2-m,所抛物线的对称轴为直线x=-$\frac{-3}{2}$-1.5,所以③正确;
当x=0时,y=x2-3x+2+m=2+m,即抛物线与y轴的交点为(0,2+m),而m>-$\frac{1}{4}$,所以二次函数y=(x-1)(x-2)+m的图象与y轴交点的一定在(0,$\frac{7}{4}$)的上方,所以④错误.
故答案为②③.
点评 本题考查了抛物线与x轴的交点问题:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
16.已知一个等腰三角形腰上的高等于底边的一半,那么腰与底边的比是( )
| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}$:1 | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:1 |
3.下列说法正确的是( )
| A. | 一组数据:4、1、3、1、2的中位数是3 | |
| B. | 了解一批节能灯的使用寿命,适合用普查的方式 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 甲、乙两人在相同条件下各射击20次,他们的成绩平均数相同,方差分别是S甲2=0.4.S乙2=0.6,则甲的射击成绩较稳定 |
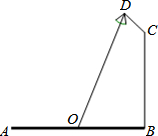 如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.
如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米. 如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象,在第一象限交于点A,连接OA,若S△AOB:S△BOC=1:2,则k的值为3.
如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象,在第一象限交于点A,连接OA,若S△AOB:S△BOC=1:2,则k的值为3.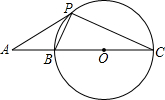 如图,点A、B、C在同一条直线上,点P在以BC为直径的⊙O上,连结PA、PB、PC,AB=BP=$\frac{1}{2}BC$.
如图,点A、B、C在同一条直线上,点P在以BC为直径的⊙O上,连结PA、PB、PC,AB=BP=$\frac{1}{2}BC$.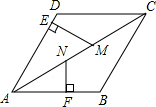 如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.
如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6. 如图,在△ABC中,AD为∠BAC的平分线,过D作DE∥AB,交AC于E点,在AB上取BF=AE,求证:FE∥BC.
如图,在△ABC中,AD为∠BAC的平分线,过D作DE∥AB,交AC于E点,在AB上取BF=AE,求证:FE∥BC.