题目内容
9．
抛物线y=-2x2+4x+1如图所示，作该抛物线关于点O对称的图形，得到一条新的抛物线，则新抛物线的解析式为y=2（x+12）-3．
分析 根据变形后抛物线的形状与原抛物线的形状相同，开口相反，然后求出抛物线y=2x2+4x-1的顶点坐标，再根据关于原点对称的点的坐标特点即可得出变形后的顶点，即可求得新抛物线的解析式．
解答 解：∵抛物线y=-2x2+4x+1可化为y=-2（x-1）2+3，
∴抛物线的顶点坐标为（1，3），
∴关于原点对称的点的坐标是（-1，-3），
∴新抛物线的解析式为y=2（x+12）-3．
故答案为y=2（x+12）-3．
点评 本题考查的是二次函数的性质和二次函数的几何变换，熟知二次函数的顶点式是解答此题的关键．
练习册系列答案
相关题目
19．计算$\sqrt{（-2-{x}^{2}）^{2}}$的结果是（ ）
| A． | -2-x2 | B． | 2+x2 | C． | -2+x2 | D． | 2-x2 |
17．下列命题中，是真命题的是（ ）
| A． | 相等的圆心角所对的弧相等，所对的弦也相等 | |
| B． | 平分弦的直径垂直于弦 | |
| C． | 依次连接四边形四边中点所组成的图形是矩形 | |
| D． | 一组邻边相等的平行四边形是菱形 |
4．下列运算中正确的是（ ）
| A． | a3•a2=a6 | B． | （a3）4=a7 | C． | a5+a5=2a5 | D． | a6÷a3=a2 |
14．下列剪纸图案中，属于中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
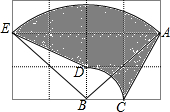如图所示，格点△ABC绕点B逆时针旋转得到△EBD，图中每个小正方形的边长是1，则图中阴影部分的面积为$\frac{7π}{4}$．
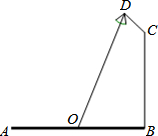如图，要在宽为22米的滨湖大道AB两边安装路灯，路灯的灯臂CD长为2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的中轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳．此时，路灯的灯柱BC高度应该设计为（11$\sqrt{3}$-4）米．
如图，已知直线y=x-2与y轴交于点C，与x轴交于点B，与反比例函数y=$\frac{k}{x}$的图象，在第一象限交于点A，连接OA，若S△AOB：S△BOC=1：2，则k的值为3．