题目内容
4.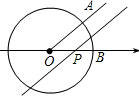 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是0<x≤$\sqrt{2}$.
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是0<x≤$\sqrt{2}$.
分析 根据题意,知直线和圆有公共点,则相切或相交.相切时,设切点为C,连接OC.根据等腰直角三角形的直角边是圆的半径1,求得斜边是$\sqrt{2}$,所以x的取值范围是0≤x≤$\sqrt{2}$.
解答 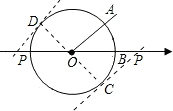 解:设切点为C,连接OC,则圆的半径OC=1,OC⊥PC,
解:设切点为C,连接OC,则圆的半径OC=1,OC⊥PC,
∵∠AOB=45°,OA∥PC,
∴∠OPC=45°,
∴PC=OC=1,
∴OP=$\sqrt{2}$,
同理,原点左侧的距离也是$\sqrt{2}$,且线段是正数,
∴x的取值范围是0<x≤$\sqrt{2}$.
故答案为:0<x≤$\sqrt{2}$.
点评 此题主要考查了直线与圆的位置关系,分别得出两圆与圆相切时求出OP的长是解决问题的关键,难度一般,注意两个极值点的寻找.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 任何两个互为相反数的数的商为-1 | |
| B. | 任何一个不是1的正数都大于它的倒数 | |
| C. | 若a>b>0,则$\frac{1}{a}>\frac{1}{b}$ | |
| D. | 若$\frac{1}{a}<-1$,则-1<a<0 |
 如图,用尺规作图作已知角∠AOB的平分线OC,其根据是构造两个三角形全等,它所用到的识别方法是SSS.
如图,用尺规作图作已知角∠AOB的平分线OC,其根据是构造两个三角形全等,它所用到的识别方法是SSS.