题目内容
8．观察下列各式：$\sqrt{3+2\sqrt{2}}$=$\sqrt{2+2\sqrt{2}+1}$=$\sqrt{（\sqrt{2}+1）^{2}}$=$\sqrt{2}$+1，$\sqrt{7+2\sqrt{10}}$=$\sqrt{5+2\sqrt{10}+2}$=$\sqrt{（\sqrt{5}+\sqrt{2}）^{2}}$=$\sqrt{5}$$+\sqrt{2}$，…由上述规律可知$\sqrt{8+2\sqrt{15}}$=$\sqrt{5}$+$\sqrt{3}$．分析 直接利用完全平方公式进而化简求出答案．
解答 解：$\sqrt{8+2\sqrt{15}}$=$\sqrt{（\sqrt{5}+\sqrt{3}）^{2}}$=$\sqrt{5}$+$\sqrt{3}$．
故答案为：$\sqrt{5}$+$\sqrt{3}$．
点评 此题主要考查了二次根式的性质与化简，正确掌握完全平方公式是解题关键．
练习册系列答案
相关题目
18．下列分式中，无论x为何值，一定有意义的是（ ）
| A． | $\frac{x-2}{x+2}$ | B． | $\frac{x-1}{x}$ | C． | $\frac{x+1}{{x}^{2}-1}$ | D． | $\frac{x-1}{{x}^{2}+5}$ |
根据给出的数轴，回答下列问题：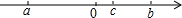
a，b，c在数轴上的位置如图所示，求|c-b|-$\sqrt{（a+b）^{2}}$-$\root{3}{（a+c）^{3}}$的值．
17．若分式$\frac{|x|-3}{{x}^{2}-6x+9}$的值为0，则x的值为（ ）
| A． | 3 | B． | -3 | C． | 3或-3 | D． | 2或3 |
如图所示，抛物线y=x2-4x+3与x轴分别交于A、B两点，交y轴于点C，