题目内容
用配方法解方程3x2-x-6=0.
考点:解一元二次方程-配方法
专题:
分析:解题时要注意解题步骤的准确应用,把左边配成完全平方式,右边化为常数.
解答:解:移项,得
3x2-x=6,
二次项系数化为1,得
x2-
x=2,
配方,得
x2-
x+
=2+
,即(x-
)2=
,
开方得:x-
=±
,
∴x1=
,x2=
.
3x2-x=6,
二次项系数化为1,得
x2-
| 1 |
| 3 |
配方,得
x2-
| 1 |
| 3 |
| 1 |
| 36 |
| 1 |
| 36 |
| 1 |
| 6 |
| 73 |
| 36 |
开方得:x-
| 1 |
| 6 |
| ||
| 6 |
∴x1=
1+
| ||
| 6 |
1-
| ||
| 6 |
点评:本题考查了解一元二次方程--配方法.用配方法解一元二次方程的步骤:
(1)形如x2+px+q=0型:第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方即可.
(2)形如ax2+bx+c=0型,方程两边同时除以二次项系数,即化成x2+px+q=0,然后配方.
(1)形如x2+px+q=0型:第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方即可.
(2)形如ax2+bx+c=0型,方程两边同时除以二次项系数,即化成x2+px+q=0,然后配方.

练习册系列答案
相关题目
 如图,Rt△ABC中∠C=90°,D为AB的中点,分别作AE∥CB、BE∥AC,两线交于点E,连接DE.作EF∥AB交CB延长线于点F,取EF中点G,连接BG.问四边形DEGB是什么特殊四边形?说明理由.
如图,Rt△ABC中∠C=90°,D为AB的中点,分别作AE∥CB、BE∥AC,两线交于点E,连接DE.作EF∥AB交CB延长线于点F,取EF中点G,连接BG.问四边形DEGB是什么特殊四边形?说明理由.
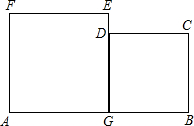 如图所示,这是一块工厂的下脚料铁板,其中AGEF和BCDG都是正方形.某个体水箱加工生产户经过计算得知,这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积(切割,焊接过程中的面积不变),他思考了一会,决定购买这块下脚料用于焊接冰箱.请你利用所学的知识帮助他设计一种最简便的切割,焊接方法,并证明你的设计方案.
如图所示,这是一块工厂的下脚料铁板,其中AGEF和BCDG都是正方形.某个体水箱加工生产户经过计算得知,这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积(切割,焊接过程中的面积不变),他思考了一会,决定购买这块下脚料用于焊接冰箱.请你利用所学的知识帮助他设计一种最简便的切割,焊接方法,并证明你的设计方案.