Question

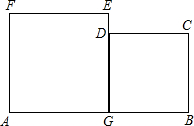如图所示，这是一块工厂的下脚料铁板，其中AGEF和BCDG都是正方形．某个体水箱加工生产户经过计算得知，这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积（切割，焊接过程中的面积不变），他思考了一会，决定购买这块下脚料用于焊接冰箱．请你利用所学的知识帮助他设计一种最简便的切割，焊接方法，并证明你的设计方案．

Answer 1

考点：作图—应用与设计作图

专题：

分析：在AG上截取AM=BC，连接FM，CM，先延长FM，CM，分别剪下△FAM和△MBC，再将△FAM和△MBC分别焊接在△FEN和△NDC的位置上，正方形MCNF就是所需的正方形铁板．先证出四边形MCNF是菱形，再证出∠NFE+∠MFE=90°，即可得出四边形MCNF是正方形．

解答：解：如上图所示：在AG上截取AM=BC，连接FM，CM，先延长FM，CM，分别剪下△FAM和△MBC，再将△FAM和△MBC分别焊接在△FEN和△NDC的位置上，正方形MCNF就是所需的正方形铁板．

证明：∵AM=BC，
∴AM=BG，
∴AM+MG=BG+MG，
∴AG=BM，
∴MG=DE，
∴EN=AM，DN=BM，
∵FM=

AM2+AF2

=MC=

BC2+MB2

，
∴FM=FN=MC=CN，
∴四边形MCNF是菱形，
∵∠MFA+∠MFE=90°，∠NFE=∠MFA，
∴∠NFE+∠MFE=90°，
∴四边形MCNF是正方形．

点评：本题主要考查了作图-应用与设计作图，解题的关键是理解题意，弄清问题中对所作图形的要求，结合对应几何图形的性质和基本作图的方法作图．