题目内容
16.已知x=2t-8,y=10-t,S=$\sqrt{xy}$,则S有最大值,这个值是3$\sqrt{2}$.分析 根据题意和已知,计算出表示xy的值的多项式,根据二次函数的性质求出xy的有最大值,得到S的最大值.
解答 解:xy=(2t-8)(10-t)
=-2t2+28t-80
=-2(t-7)2+18
-2<0,∴函数xy有最大值18,
则S有最大值3$\sqrt{2}$
故答案为:大;3$\sqrt{2}$.
点评 本题考查的是二次函数的最值问题,根据题意列出关于x的函数关系式是解题的关键,解答时,根据二次函数的性质,确定有最大或小值,并用配方法或公式法求出最值.

练习册系列答案
相关题目
7.有下列说法:①如果两直线都与第三条直线平行,那么这两条直线也互相平行.②直线外一点到这条直线的垂线段,叫做点到直线的距离.③△ABC在平移过程中周长不变.④三角形的中线、角平分线、高线都在三角形内部.其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.菱形中较长的对角线与边长的比为$\sqrt{3}:1$,则菱形的四个角为( )
| A. | 30°,30°,150°,150° | B. | 45°,45°,135°,135° | ||
| C. | 60°,60°,120°,120° | D. | 90°,90°,90°,90° |
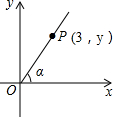 如图,直角坐标系中,P(3,y)是第一象限内的点,且$tanα=\frac{4}{3}$,求sinα.
如图,直角坐标系中,P(3,y)是第一象限内的点,且$tanα=\frac{4}{3}$,求sinα. 如图,AB∥CD,BC平分∠ECD交AB于点B,若∠EAB=60°,则∠BCD=30°.
如图,AB∥CD,BC平分∠ECD交AB于点B,若∠EAB=60°,则∠BCD=30°.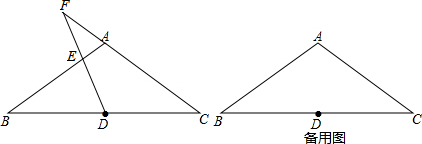
 如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足为E.若∠BAD=30°,且BE=2,则CD=4$\sqrt{3}$.
如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足为E.若∠BAD=30°,且BE=2,则CD=4$\sqrt{3}$.