题目内容
14. 二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:①4ac-b2<0;
②3b+2c<0;
③4a+c<2b;
④m(am+b)+b<a(m≠-1).
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由图象开口向下可以得到a<0;图象与x轴有两个交点则b2-4ac>0;对称轴为直线x=-1;当x=1时,y<0;通过这些条件,结合对函数解析式的变式分析就可以得出结果.
解答 解:∵图象与x轴有两个交点,
∴b2-4ac>0,
所以①正确;
∵图象的对称轴为直线x=-1,
∴$-\frac{b}{2a}$=-1,解得b=2a,
∵从图象可知,当x=1时,y<0,
∴a+b+c<0
2a+2b+2c<0
3b+2c<0,
所以②正确;
∵图象的对称轴为直线x=-1,当x=0时,y=c>0
∴当x=-2时,y>0
∴4a-2b+c>0 则有4a+c>2b
所以③错误;
由式子④整理得am2+bm+b-a<0
把b=2a代入得 am2+2am+a<0
在不等式两边都除以a,由于抛物线开口向下,故a<0,则不等号方向应改变,整理得
m2+2m+1>0 配方得 (m+1)2>0
∵m≠-1
∴(m+1)2>0成立
所以④正确.
故选:C.
点评 本题考查了二次函数的解析式与图象的关系,解答此题的关键是要明确a的符号决定了抛物线开口方向;通过对称轴可得到a与b的关系;抛物线与x轴的交点个数,决定了b2-4ac的符号.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
4. 如图是一个正方体的平面展开图,则和“你”相对的面上的汉字是( )
如图是一个正方体的平面展开图,则和“你”相对的面上的汉字是( )
 如图是一个正方体的平面展开图,则和“你”相对的面上的汉字是( )
如图是一个正方体的平面展开图,则和“你”相对的面上的汉字是( )| A. | 考 | B. | 试 | C. | 顺 | D. | 利 |
2.如果a>b,c≠0,那么下列不等式成立的是( )
| A. | a-c>b-c | B. | c-a>c-b | C. | ac>bc | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
19. 如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于( )
如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于( )
 如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于( )
如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于( )| A. | 61° | B. | 51° | C. | 50° | D. | 60° |
3.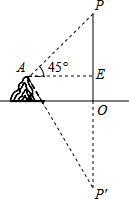 在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
 在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )| A. | $25\sqrt{3}+75$ | B. | $50\sqrt{3}+50$ | C. | $75\sqrt{3}+75$ | D. | $50\sqrt{3}+100$ |
 如图,菱形ABCD中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为24,则OE的长等于( )
如图,菱形ABCD中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为24,则OE的长等于( ) 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.