题目内容
4. 如图,点A的坐标为(1,0),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.
如图,点A的坐标为(1,0),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.
分析 当线段AB最短时,AB与直线y=2x+4垂直,设直线与坐标轴的交点为C、D,作AB′⊥CD,根据解析式即可求得C、D的坐标,然后根据勾股定理求得CD,然后根据三角形相似即可求得AB的最短长度.
解答 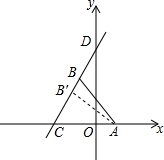 解:由直线y=2x+4可知,直线与坐标轴的交点为C(-2,0),D(0,4),
解:由直线y=2x+4可知,直线与坐标轴的交点为C(-2,0),D(0,4),
∴OC=2,OD=4,
∴CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=2$\sqrt{5}$,
∵点A的坐标为(1,0),
∴AC=2+1=3,
∵∠ACB′=∠DCO,∠ABC=∠DOC=90°,
∴△AB′C∽△DOC,
∴$\frac{AB}{OD}$=$\frac{AC}{CD}$,即$\frac{AB′}{4}$=$\frac{3}{2\sqrt{5}}$,
∴AB′=$\frac{6}{5}$$\sqrt{5}$.
故答案为$\frac{6}{5}$$\sqrt{5}$.
点评 本题考查了垂线段最短的性质,一次函数图象上点的坐标特征,勾股定理的应用,三角形相似的判定和性质,熟知垂线段最短是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.等腰三角形的周长为10,底边长y与腰x的函数关系式是y=10-2x,则自变量x的取值范围是( )
| A. | x>0 | B. | x<5 | C. | 0<x<5 | D. | 2.5<x<5 |
19.下列各式的恒等变形属于分解因式的是( )
| A. | (x+2)(x-2)=x2-4 | B. | x2-9+x=(x+3)(x-3)+x | ||
| C. | 3x2-5x=2x(x-2)+x2-x | D. | x2-2xy+y2=(x-y)2 |
9.如果关于x的方程(m+1)x2+(m-1)x+m=0是一元一次方程,则m的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 1或-1 |
13.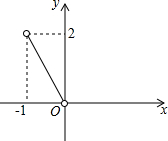 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )
 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )| A. | y=-2x | B. | y=-2x(-1<x<0) | C. | y=-$\frac{1}{2}$x | D. | y=-$\frac{1}{2}$x(-1<x<0) |
 如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,并且BE=CF,求证:点D在BC的垂直平分线上.
如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,并且BE=CF,求证:点D在BC的垂直平分线上.