Question

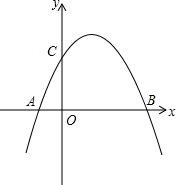如图，抛物线y=

1

2

x2+

2

2

x+2，与x轴交于A、B两点，于y轴交于点C．
（1）求A、B、C三点的坐标．
（2）求此抛物线的顶点坐标、对称轴．它有最大值还是最小值？是多少？
（3）证明△ABC为直角三角形．
（4）当x为何值时，y＞0，y=0，y＜0．
（5）在抛物线上，除点C外，是否还存在另一动点P，使△ABP是直角三角形？若存在，请求出点P的坐标；若不存在，说明理由．

Answer 1

考点：二次函数综合题

专题：

分析：（1）令y=0，解关于x的一元二次方程即可得到点A、B的坐标，令x=0求出y的值即可得到点C的坐标；
（2）把抛物线解析式整理成顶点式形式，然后写出顶点坐标，对称轴以及最值；
（3）利用勾股定理列式求出AC、BC，再利用勾股定理逆定理判断即可；
（4）根据二次函数图象与不等式的关系分别写出即可；
（5）根据二次函数对称性，点C关于对称轴的对称点即为所求的点P．

解答：（1）解：令y=0，则-

1

2

x²+

2

2

x+2=0，
整理得，x²-

2

x-4=0，
解得x₁=-

2

，x₂=2

2

，
所以，A（-

2

，0），B（2

2

，0），
令x=0，则y=2，
所以，点C（0，2）；

（2）解：∵y=-

1

2

x²+

2

2

x+2=-

1

2

（x-

2

2

）²+

9

4

，
所以，顶点坐标为（

2

2

，

9

4

），
对称轴是直线x=

2

2

，
有最大值，最大值是

9

4

；

（3）证明：AC=

( 2 )2+22

=

6

，
BC=

(2 2 )2+22

=2

3

，
AB=2

2

-（-

2

）=3

2

，
∵AC²+BC²=（

6

）²+（2

3

）²=18，
AB²=（3

2

）²=18，
∴AC²+BC²=AB²，
∴△ABC是直角三角形；

（4）解：当-

2

＜x＜2

2

时，y＞0，
当x=-

2

或x-2

2

时，y＞0，
当x＜-

2

或x＞2

2

时，y＜0；

（5）解：存在点P，且P点与C点，关于抛物线的对称轴对称，
∵点C（0，2），对称轴为直线x=

2

2

，
∴点P的横坐标为2×

2

2

-0=

2

，
∴P（

2

，2）．

点评：本题是二次函数综合题型，主要利用了抛物线与坐标轴的交点的求解，二次函数的顶点坐标、对称轴以及最值问题，勾股定理和勾股定理逆定理，二次函数与不等式．