题目内容
2.在Rt△ABC中,∠C=90°,cosA=$\frac{1}{3}$,AC=2,那么BC=4$\sqrt{2}$.分析 根据∠C=90°,得出cosA=$\frac{AC}{AB}$,再根据AC=2,求出AB,最后根据勾股定理即可求出BC.
解答  解:∵∠C=90°,
解:∵∠C=90°,
∴cosA=$\frac{AC}{AB}$=$\frac{1}{3}$,
∵AC=2,
∴AB=6,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{36-4}$=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查了解直角三角形,用到的知识点锐角三角函数、勾股定理,关键是根据题意求出AB.

练习册系列答案
相关题目
17.在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判定DE∥BC的是( )
| A. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | $\frac{DB}{EC}$=$\frac{AB}{AC}$ | D. | $\frac{AD}{DB}$=$\frac{DE}{BC}$ |
12.在同一平面直角坐标系内,将函数y=x-3的图象向右平移2个单位,再向下平移1个单位得到的图象与x轴的交点坐标是( )
| A. | (-6,0) | B. | (2,0) | C. | (6,0) | D. | (-1,0) |
 如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.求证:AF=CE.
如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.求证:AF=CE.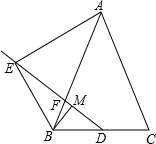 如图,已知在△ABC中AB=AC,点D为BC边的中点,点F在边AB上,点E在线段DF的延长线上,且∠BAE=∠BDF,点M在线段DF上,且∠EBM=∠C.
如图,已知在△ABC中AB=AC,点D为BC边的中点,点F在边AB上,点E在线段DF的延长线上,且∠BAE=∠BDF,点M在线段DF上,且∠EBM=∠C. 如图,数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,若原点O是线段AC上的任意一点,那么a+b-2c=0.
如图,数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,若原点O是线段AC上的任意一点,那么a+b-2c=0.