题目内容
20. 如图,?ABCD的对角线AC、BD相交于点O,点E是BC的中点,若△ABD的周长为8cm,则△BOE的周长是4cm.
如图,?ABCD的对角线AC、BD相交于点O,点E是BC的中点,若△ABD的周长为8cm,则△BOE的周长是4cm.
分析 根据平行四边形的对边相等和对角线互相平分可得,BC=AD,DC=AB,DO=BO,E点是CD的中点,可得OE是△BCD的中位线,可得OE=$\frac{1}{2}$BC.从而得到结果是4cm.
解答 解:∵四边形ABCD是平行四边形,
∴O是BD中点,△ABD≌△CDB,
又∵E是CD中点,
∴OE是△BCD的中位线,
∴OE=$\frac{1}{2}$AB,
即△BOE的周长=$\frac{1}{2}$△ABD的周长,
∴△BOE的周长=$\frac{1}{2}$△ABD的周长.
∴△DOE的周长=$\frac{1}{2}$×8cm=4cm.
故答案为:4.
点评 本题主要考查平行四边形的性质及三角形中位线的性质的应用.

练习册系列答案
相关题目
16.某学习小组10名学生参加数学竞赛,他们的得分情况如下表:
那么这10名学生所得分数的众数和中位数分别是( )
| 人数(人) | 2 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
17.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{10}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
8.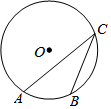 已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
 已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )| A. | 30° | B. | 35° | C. | 40° | D. | 60° |
15.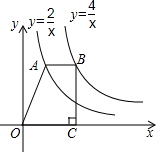 如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )
如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )
 如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )
如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.多项式ab-bc+a2-c2分解因式的结果是( )
| A. | (a-c)(a+b+c) | B. | (a-c)(a+b-c) | C. | (a+c)(a+b-c) | D. | (a+c)(a-b+c) |
10.因式分解与整数乘法一样,都是一种恒等变形,即在变形的过程中,形变值不变,于是将多项式x2-y2+(2x+2y)分解因式的结果为( )
| A. | (x+y)(x-y+2) | B. | (x+y)(x-y-2) | C. | (x-y)(x-y+2) | D. | (x-y)(x-y-2) |