题目内容
15.若正比例函数的图象经过(-3,2),则这个图象一定经过点( )| A. | (2,-3) | B. | $({\frac{3}{2},-1})$ | C. | (-1,1) | D. | (2,-2) |
分析 先利用待定系数法求出正比例函数的解析式,再把各选项代入进行检验即可.
解答 解:设正比例函数的解析式为y=kx(k≠0),
∵正比例函数的图象经过(-3,2),
∴-3k=2,解得k=-$\frac{2}{3}$,
∴正比例函数的解析式为:y=-$\frac{2}{3}$x.
A、∵当x=2时,y=-$\frac{2}{3}$×2=-$\frac{4}{3}$≠-3,∴此点不在函数图象上,故本选项错误;
B、∵当x=$\frac{3}{2}$时,y=-$\frac{2}{3}$×$\frac{3}{2}$=-1,∴此点在函数图象上,故本选项正确;
C、∵当x=-1时,y=-$\frac{2}{3}$×(-1)=$\frac{2}{3}$≠1,∴此点不在函数图象上,故本选项错误;
D、∵当x=2时,y=-$\frac{2}{3}$×2=-$\frac{4}{3}$≠-2,∴此点不在函数图象上,故本选项错误.
故选B.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.因式分解与整数乘法一样,都是一种恒等变形,即在变形的过程中,形变值不变,于是将多项式x2-y2+(2x+2y)分解因式的结果为( )
| A. | (x+y)(x-y+2) | B. | (x+y)(x-y-2) | C. | (x-y)(x-y+2) | D. | (x-y)(x-y-2) |
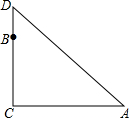 如图,在一棵树CD的10m高处B有两只猴子,其中一只猴子爬下树走到离树20m处的池塘的A处,另一只爬到树顶D后直接跃到A处,距离以直线计算.如果两只猴子所经过的距离相等,请问这棵树有多高?
如图,在一棵树CD的10m高处B有两只猴子,其中一只猴子爬下树走到离树20m处的池塘的A处,另一只爬到树顶D后直接跃到A处,距离以直线计算.如果两只猴子所经过的距离相等,请问这棵树有多高?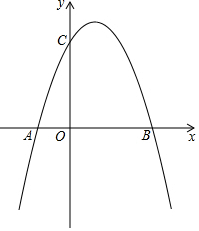 如图,抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-1,0),B(3,0),与y轴交于点C(0,3).
如图,抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-1,0),B(3,0),与y轴交于点C(0,3).