题目内容
18.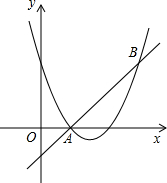 如图,直线y=x-1和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
如图,直线y=x-1和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).(1)求抛物线的解析式;
(2)求不等式x2+bx+c<x-1的解集(直接写出答案).
(3)抛物线分别与x轴,y轴交于点C,D,在抛物线对称轴上有一点P,使PB+PC的值最小,请你求出这个最小值.
分析 (1)直接将A,B两点代入函数解析式求出答案;
(2)直接利用两函数图象结合其交点得出x的取值范围;
(3)结合利用轴对称求最短路线的方法得出P点位置,再利用勾股定理得出答案.
解答  解:(1)将A(1,0),B(3,2),代入y=x2+bx+c得:
解:(1)将A(1,0),B(3,2),代入y=x2+bx+c得:
$\left\{\begin{array}{l}{1+b+c=0}\\{9+3b+c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-3}\\{c=2}\end{array}\right.$,
故抛物线解析式为:y=x2-3x+2;
(2)∵直线y=x-1和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),
∴不等式x2+bx+c<x-1的解集为:1<x<3;
(3)由题意可得:点P在AB上时,此时PB+PC=AB最小,
过点B作BE⊥x轴于点E,
可得BE=2,AE=3-1=2,
则AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
点评 此题主要考查了二次函数与不等式一级利用轴对称求最短路径,正确得出P点位置是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.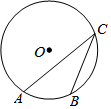 已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
 已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )| A. | 30° | B. | 35° | C. | 40° | D. | 60° |
9.多项式ab-bc+a2-c2分解因式的结果是( )
| A. | (a-c)(a+b+c) | B. | (a-c)(a+b-c) | C. | (a+c)(a+b-c) | D. | (a+c)(a-b+c) |
13.$\sqrt{7}$ 是一个无理数,请估计$\sqrt{7}$在哪两个整数之间?( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
10.因式分解与整数乘法一样,都是一种恒等变形,即在变形的过程中,形变值不变,于是将多项式x2-y2+(2x+2y)分解因式的结果为( )
| A. | (x+y)(x-y+2) | B. | (x+y)(x-y-2) | C. | (x-y)(x-y+2) | D. | (x-y)(x-y-2) |