题目内容
7．某公司要求招甲、乙两种工作人员30人，甲种工作人员月薪6000元，乙种工作人员月薪10000元．现要求每月的工资不能超过22万元，问至多可招乙种工作人员多少名？分析 设可招乙种工作人员x名，则甲种工作人员（30-x）名，根据甲乙的工资以及每月的工资不能超过22万元，列不等式求解．
解答 解：设可招乙种工作人员x名，则甲种工作人员（30-x）名，
由题意得，10000x+6000（30-x）≤220000，
解得：x≤10．
答：至多可招乙种工作人员10名．
点评 本题考查了一元一次不等式的应用，解答本题的关键是读懂题意，设出未知数，找出合适的不等关系，列不等式求解．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
17．已知△ABC和△DEF全等，∠A=40°，∠B=50°，则∠D的度数为（ ）
| A． | 40° | B． | 50° | C． | 90° | D． | 40°或50°或90° |
18．
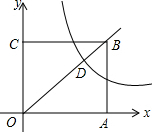如图，双曲线y=$\frac{3}{x}$与矩形OABC的对角线OB相交于点D，且DB：OD=2：3，则矩形OABC的面积为（ ）
如图，双曲线y=$\frac{3}{x}$与矩形OABC的对角线OB相交于点D，且DB：OD=2：3，则矩形OABC的面积为（ ）| A． | $\frac{25}{3}$ | B． | $\frac{22}{3}$ | C． | $\frac{23}{3}$ | D． | 8 |
17．下面的计算错误的是（ ）
| A． | a3•a3=a6 | B． | （-y2）5=y10 | ||
| C． | （-a3y2）3=-a9y6 | D． | （$\frac{1}{3}$x-$\frac{3}{4}$xy）•（-12y）=-4xy+9xy2 |