题目内容
20.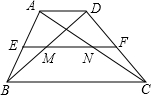 如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.
如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.(1)求证:MN=$\frac{1}{2}$(BC-AD);
(2)若上底AD=8,MN=3,求EF及BC的长.
分析 (1)根据梯形的中位线性质得到EF∥AD∥BC,AE=BE,DF=CF,则可判断EM为△BAD的中位线,所以EM=$\frac{1}{2}$AD,同理可得EN=$\frac{1}{2}$BC,把两式相减即可得到结论;
(2)利用(1)的结论可计算出BC,然后根据梯形的中位线性质计算EF的长.
解答 (1)证明:∵EF为梯形的中位线,
∴EF∥AD∥BC,AE=BE,DF=CF,
∵EM∥AD,BE=AE,
∴EM为△BAD的中位线,
∴EM=$\frac{1}{2}$AD,
同理可得EN=$\frac{1}{2}$BC,
∴EN-EM=$\frac{1}{2}$BC-$\frac{1}{2}$AD,
∴MN=$\frac{1}{2}$(BC-AD);
(2)解:∵MN=$\frac{1}{2}$(BC-AD);,
即3=$\frac{1}{2}$(BC-8),
∴BC=14,
∴EF=$\frac{1}{2}$(AD+BC)=$\frac{1}{2}$×(8+14)=11.
点评 本题考查了梯形的中位线:连接梯形两腰中点的线段叫做梯形的中位线.梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.也考查了三角形中位线性质.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
10.将1、2、3三个数字分别作为横坐标和纵坐标,随机生成的点的坐标如下表.如果每个点出现的可能性相等,那么从中任意取一点,则这个点的函数y=x图象上的概率是$\frac{1}{3}$.
| (1,1) | (1,2) | (1,3) |
| (2,1) | (2,2) | (2,3) |
| (3,1) | (3,2) | (3,3) |
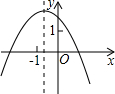
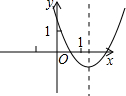
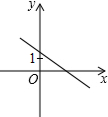 已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是( )
已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是( )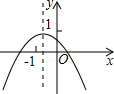
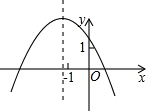
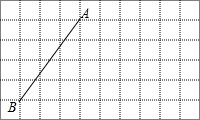 如图是l0×6的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上.
如图是l0×6的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上.