题目内容
5.求代数式$\frac{x-y}{x}$÷(x-$\frac{2xy-{y}^{2}}{x}$)的值,其中x=2tan45°,y=-2sin30°.分析 首先把括号里面通分,然后再约分计算,计算出x、y的值,再代入即可得到代数式的值.
解答 解:原式=$\frac{x-y}{x}$÷($\frac{{x}^{2}}{x}$-$\frac{2xy-{y}^{2}}{x}$),
=$\frac{x-y}{x}$×$\frac{x}{(x-y)^{2}}$,
=$\frac{1}{x-y}$,
∵x=2tan45°,y=-2sin30°,
∴x=2,y=-1,
把x=2,y=-1代入上式可得:原式=$\frac{1}{2+1}$=$\frac{1}{3}$.
点评 此题主要考查了特殊角的三角函数,以及分式的化简求值,关键是正确把代数式进行化简.

练习册系列答案
相关题目
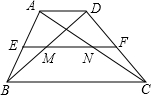 如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.
如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.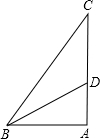 如图,在Rt△ABC中,∠CAB=90°,sinC=$\frac{3}{5}$,AC=6,BD平分∠CBA交AC边于点D.求:
如图,在Rt△ABC中,∠CAB=90°,sinC=$\frac{3}{5}$,AC=6,BD平分∠CBA交AC边于点D.求: