题目内容
12．
如图，则a=9．
分析 利用勾股定理进行计算即可．
解答 解：由勾股定理可知：a=$\sqrt{4{1}^{2}-4{0}^{2}}$=9．
故答案为：9．
点评 本题主要考查的是勾股定理的应用，掌握勾股定理是解题的关键．
练习册系列答案
相关题目
20．
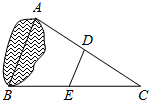如图，A、B两地间有一池塘阻隔，为测量A、B两地的距离，在地面上选一点C，连接CA、CB的中点D、E，若DE的长度为30m，则A，B两地的距离是（ ）
如图，A、B两地间有一池塘阻隔，为测量A、B两地的距离，在地面上选一点C，连接CA、CB的中点D、E，若DE的长度为30m，则A，B两地的距离是（ ）| A． | 15m | B． | 30m | C． | 60m | D． | 90m |
7．
二次函数y=ax2+b的图象如图所示，则下列判断正确的是（ ）
二次函数y=ax2+b的图象如图所示，则下列判断正确的是（ ）| A． | a＞0，b＜0 | B． | a＞0，b＞0 | C． | a＜0，b＜0 | D． | a＜0，b＞0 |
17．
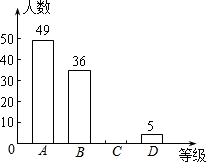近年来，校园安全问题引起了社会的极大关注，为了让学生了解安全知识，增强安全意识，某校举行了一次“安全知识竞赛”．为了了解这次竞赛的成绩（取整数）情况，从中抽取了部分学生的成绩为一个样本，绘制了如下不完整统计图、表（说明：A级：90分-100分；B级：75分-89分；C级：60分-74分；D级：60分以下）．
请结合统计图、表中提供的信息，解答下列问题：
（1）统计表中m=10，n=0.05，并把条形统计图补充完整．
（2）本次竞赛的中位数落在B级；
（3）若该校共有2000名学生，请你用此样本估计安全知识竞赛中A级和B级的学生共有多少人？
近年来，校园安全问题引起了社会的极大关注，为了让学生了解安全知识，增强安全意识，某校举行了一次“安全知识竞赛”．为了了解这次竞赛的成绩（取整数）情况，从中抽取了部分学生的成绩为一个样本，绘制了如下不完整统计图、表（说明：A级：90分-100分；B级：75分-89分；C级：60分-74分；D级：60分以下）．| 类别 | 频数 （人数） | 频率 |
| A | 49 | 0.49 |
| B | 36 | 0.36 |
| C | m | 0.1 |
| D | 5 | n |
（1）统计表中m=10，n=0.05，并把条形统计图补充完整．
（2）本次竞赛的中位数落在B级；
（3）若该校共有2000名学生，请你用此样本估计安全知识竞赛中A级和B级的学生共有多少人？
4．
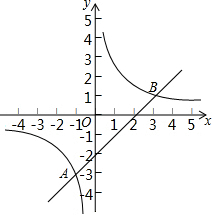已知一次函数y1=kx+b（k＞0）与反比例函数y2=$\frac{m}{x}$（m≠0）的图象相交于A（-1，a），B（3，b）两点，当y1＞y2时，实数x的取值范围是（ ）
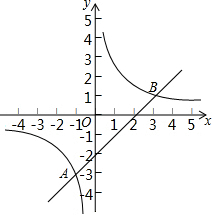已知一次函数y1=kx+b（k＞0）与反比例函数y2=$\frac{m}{x}$（m≠0）的图象相交于A（-1，a），B（3，b）两点，当y1＞y2时，实数x的取值范围是（ ）| A． | x＜-1或0＜x＜3 | B． | -1＜x＜0或0＜x＜3 | C． | -1＜x＜0或x＞3 | D． | 0＜x＜3 |
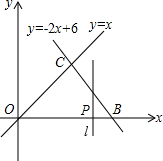如图，直线OC，BC的解析式分别为y=x和y=-2x+6，动点P（t，0）在线段OB上移动（不与O，B重合），过点P作直线l与x垂直．