题目内容
5．不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1＜2-2x}\end{array}\right.$的解集是-1≤x＜1．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：解不等式x≤3x+2，得：x≥-1，
解不等式x-1＜2-2x，得：x＜1，
∴不等式组的解集为：-1≤x＜1，
故答案为：-1≤x＜1．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
20．与4-$\sqrt{6}$最接近的整数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
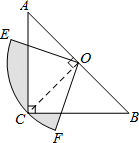如图，在△ABC中，∠C=90°，AC=BC，斜边AB=4，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形OEF，弧EF经过点C，则图中阴影部分的面积为π-2平方单位．
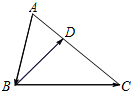如图，在△ABC中，点D在AC边上且AD：DC=1：2，若$\overrightarrow{AB}=\overrightarrow{m}$，$\overrightarrow{BD}=\overrightarrow{n}$，那么$\overrightarrow{DC}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$（用向量$\overrightarrow{m}$、$\overrightarrow{n}$表示）．
14．方程组$\left\{\begin{array}{l}{2x+y=3}\\{3x-z=7}\\{x-y+3z=0}\end{array}\right.$的解为（ ）
| A． | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{y=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=1}\end{array}\right.$ |
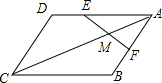如图，AC是?ABCD的对角线，点E在AD上，AE=2DE，点F是AB的中点，连接EF交AC于点M，若AC=14，则AM=4．