题目内容
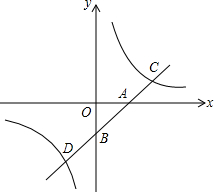 如图,直线y=kx+b分别交x轴,y轴于A、B两点,与双曲线y=
如图,直线y=kx+b分别交x轴,y轴于A、B两点,与双曲线y=| m |
| x |
(1)k和b;
(2)m(精确到0.01)
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)求出B的坐标,根据待定系数法即可求得k、b的值.
(2)作CE⊥x轴于点E.易得到△CAE为等腰直角三角形.就可求得C的坐标,据待定系数法就可求得m的值;
(2)作CE⊥x轴于点E.易得到△CAE为等腰直角三角形.就可求得C的坐标,据待定系数法就可求得m的值;
解答:
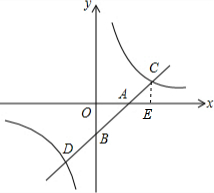 解:(1)∵OA=OB,A点的坐标为(2,0).
解:(1)∵OA=OB,A点的坐标为(2,0).
∴点B的坐标为(0,-2),
代入y=kx+b,得
,解得
.
(2)作CE⊥x轴于点E.易得到△CAE为等腰直角三角形.
∵AC=OA=2,那么AE=2×cos45°=
,那么OE=2+
,那么点C坐标为(2+
,
).
代入y=
得
=
,解得m=2+2
.
 解:(1)∵OA=OB,A点的坐标为(2,0).
解:(1)∵OA=OB,A点的坐标为(2,0).∴点B的坐标为(0,-2),
代入y=kx+b,得
|
|
(2)作CE⊥x轴于点E.易得到△CAE为等腰直角三角形.
∵AC=OA=2,那么AE=2×cos45°=
| 2 |
| 2 |
| 2 |
| 2 |
代入y=
| m |
| x |
| 2 |
| m | ||
2+
|
| 2 |
点评:本题考查用待定系数法求函数解析式,解题关键是利用所给条件得到关键点的坐标,进而求得函数解析式

练习册系列答案
相关题目
南宁地铁1号线一期工程西起石埠,东至南宁东站,全线采用地下线方式铺设,线路长32.1公里.32.1公里可用科学记数法可表示为( )米.
| A、0.321×105 |
| B、3.21×104 |
| C、32.1×103 |
| D、3.21×103 |
若一个正n边形的一个外角为45°,则n等于( )
| A、6 | B、8 | C、10 | D、12 |
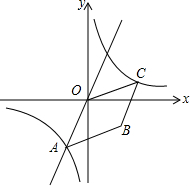 如图,已知正比例函数y=2x与反比例函数的图象交于点A(m,-2)
如图,已知正比例函数y=2x与反比例函数的图象交于点A(m,-2)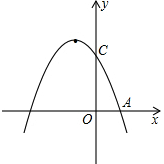 已知:如图,抛物线y=-x2-2x+m与x轴交于A(1,0)点,与y轴交于点C,另有一条直线l的解析式为y=2x+n.
已知:如图,抛物线y=-x2-2x+m与x轴交于A(1,0)点,与y轴交于点C,另有一条直线l的解析式为y=2x+n.