题目内容
若一个正n边形的一个外角为45°，则n等于（ ）
| A、6 | B、8 | C、10 | D、12 |
考点：多边形内角与外角
专题：
分析：根据多边形的外角和是360°，正多边形的每个外角都相等，即可求得．
解答：解：∵多边形的外角和为360°，一个外角45°，
∴多边形得到边数360÷45=8，所以是八边形．
故选B．
∴多边形得到边数360÷45=8，所以是八边形．
故选B．
点评：本题考查多外角和边形的为360°，正确理解多边形外角和定理是关键．
练习册系列答案
相关题目
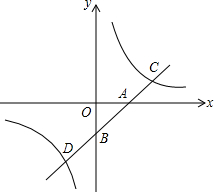如图，直线y=kx+b分别交x轴，y轴于A、B两点，与双曲线y=
已知AB=BF，AD⊥EC，求证：BC=EB．
如图，小马虎设计了某个产品的包装盒，由于粗心少设计了其中的一部分，请你帮他补上是该图形能折面一个密封的正方体的盒子，共有
在直角坐标系中，如图有△ABC，现另有一点D满足以A、B、D为顶点的三角形与△ABC全等，则D点坐标为用尺规作图，下列条件能作出唯一三角形的有（ ）
①已知两锐角；②已知两边及夹角；③已知三边；④已知两角及一边．
①已知两锐角；②已知两边及夹角；③已知三边；④已知两角及一边．
| A、1个 | B、2个 | C、3个 | D、4个 |
如图所示，平行四边形ABCD中，AC，BD相交与点O，E，F在对角线BD上，且BE=DF，试说明四边形AECF的形状．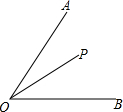
如图，∠AOB=45°，角内一点P，PO=10，两边上各有点Q，R（均不同于O），则△PQR的周长的最小值为