题目内容
14.设A=$\frac{a-2}{{1+2a+{a^2}}}$÷(a-$\frac{3a}{a+1}}$).(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);…
解关于x的不等式:$\frac{x-2}{2}$-$\frac{7-x}{4}$≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
分析 (1)根据分式的除法和减法可以解答本题;
(2)根据(1)中的结果可以解答题目中的不等式并在数轴上表示出不等式的解集.
解答 解:(1)A=$\frac{a-2}{{1+2a+{a^2}}}$÷(a-$\frac{3a}{a+1}}$)
=$\frac{a-2}{(a+1)^{2}}÷\frac{a(a+1)-3a}{a+1}$
=$\frac{a-2}{(a+1)^{2}}•\frac{a+1}{{a}^{2}-2a}$
=$\frac{a-2}{(a+1)^{2}}•\frac{a+1}{a(a-2)}$
=$\frac{1}{a(a+1)}$
=$\frac{1}{{a}^{2}+a}$;
(2)∵a=3时,f(3)=$\frac{1}{{3}^{2}+3}=\frac{1}{12}$,
a=4时,f(4)=$\frac{1}{{4}^{2}+4}=\frac{1}{20}$,
a=5时,f(5)=$\frac{1}{{5}^{2}+5}=\frac{1}{30}$,
…
∴$\frac{x-2}{2}$-$\frac{7-x}{4}$≤f(3)+f(4)+…+f(11),
即$\frac{x-2}{2}$-$\frac{7-x}{4}$≤$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{11×12}$
∴$\frac{x-2}{2}$-$\frac{7-x}{4}$≤$\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}$+…+$\frac{1}{11}-\frac{1}{12}$,
∴$\frac{x-2}{2}$-$\frac{7-x}{4}$≤$\frac{1}{3}-\frac{1}{12}$,
∴$\frac{x-2}{2}$-$\frac{7-x}{4}$≤$\frac{1}{4}$,
解得,x≤4,
∴原不等式的解集是x≤4,在数轴上表示如下所示, .
.
点评 本题考查分式的混合运算、在数轴表示不等式的解集、解一元一次不等式,解答本题的关键是明确分式的混合运算的计算方法和解不等式的方法.

 名校课堂系列答案
名校课堂系列答案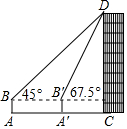 如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,$\sqrt{2}$≈1.414)( )
如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,$\sqrt{2}$≈1.414)( )| A. | 34.14米 | B. | 34.1米 | C. | 35.7米 | D. | 35.74米 |
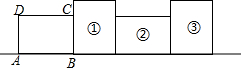 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )| A. | 2017π | B. | 2034π | C. | 3024π | D. | 3026π |
| A. | 2 | B. | 3 | C. | 5 | D. | 7 |
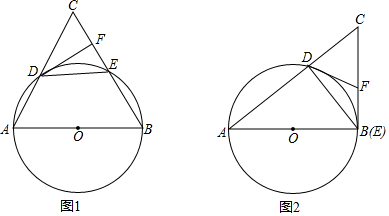
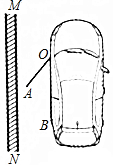 如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米.已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin40°≈0.64;cos40°≈0.77;tan40°≈0.84)
如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米.已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin40°≈0.64;cos40°≈0.77;tan40°≈0.84)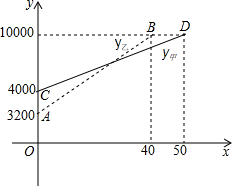 2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:
2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题: