题目内容
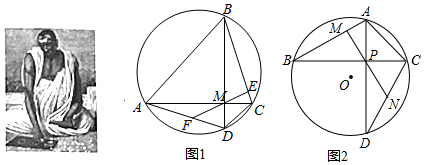
1.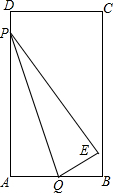 如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ
如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ(1)用含t的代数式表示AP=6-t,AQ=$\frac{2}{3}$+t;
(2)连接BD,在运动过程中,当△PQE∽△BDC时,求t的值;
(3)在运动的过程中,∠PQE能否等于∠ABD的一半?若能,求出相应的t值;若不能,说明理由.(参考数据:$\sqrt{2}$=1.4,$\sqrt{3}$=1.7,$\sqrt{5}$=2.2)
分析 (1)由题意可知:点P运动t秒时,点Q运动了($\frac{2}{3}$+t)秒,根据时间×速度得到运动的距离,即线段的长;
(2)由△PQE≌△PQA和△PQE∽△BDC,得:△PQA∽△BDC,列比例式可得:AP=2AQ,列式可得结论;
(3)如图2,根据角的关系得:EQ∥BD,根据三角函数表示AH的长和PH的长,由AH=AP+PH列式可得结论.
解答 解:(1)由题意得:DP=t,AQ=$\frac{2}{3}$+t,
∴AP=AD-DP=6-t,
故答案为:6-t;$\frac{2}{3}$+t;
(2)如图1,由折叠得:△PQE≌△PQA,
当△PQE∽△BDC时,
得:△PQA∽△BDC,
∴$\frac{PA}{BC}=\frac{AQ}{DC}$,
∴$\frac{AP}{AQ}=\frac{BC}{DC}$,
∵四边形ABCD是矩形,
∴BC=AD=6,DC=AC=3,
∴$\frac{AP}{AQ}=\frac{6}{3}$=2,
∴AP=2AQ,
即6-t=2($\frac{2}{3}$+t),
t=$\frac{14}{9}$;
(3)如图2,由折叠得:∠PQE=∠AQP,
当∠PQE=$\frac{1}{2}$∠ABD时,2∠PQE=∠ABD,
∴∠EQA=∠ABD,
∴EQ∥BD,
延长QE交AD于H,
tan∠ABD=tan∠EQA=$\frac{AD}{AB}=\frac{6}{3}$=2,
∴$\frac{AH}{AQ}=2$,
∴AH=2($\frac{2}{3}$+t)=$\frac{4}{3}$+2t,
∵QH∥BD,
∴∠AHQ=∠ADB,
∴sin∠AHQ=$\frac{PE}{PH}$=sin∠ADB=$\frac{AB}{BD}$,
∴$\frac{6-t}{PH}=\frac{3}{\sqrt{{6}^{2}+{3}^{2}}}$,
PH=$\sqrt{5}$(6-t),
由AP+PH=AH得:6-t+$\sqrt{5}$(6-t)=$\frac{4}{3}$+2t,
t=$\frac{6+6\sqrt{5}-\frac{4}{3}}{3+\sqrt{5}}$=$\frac{\frac{40}{3}\sqrt{5}-16}{4}$,
解得:t=$\frac{10}{3}$;
∵动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,且点P的运动时间为t(秒).
∴t+$\frac{2}{3}$≤3,
∴t≤$\frac{7}{3}$,
∵$\frac{10}{3}$>$\frac{7}{3}$,
所以在运动的过程中,∠PQE不能等于∠ABD的一半.
点评 本题是四边形的综合题,考查了折叠的性质、三角形相似的性质和判定、矩形的性质、三角函数以及动点运动问题,要特别注意本题的两个问题:①两个动点不是同时出发,有时间差$\frac{2}{3}$,②设点P的运动时间为t(秒);正确表示动点P、Q两点的路程是关键.

 名校课堂系列答案
名校课堂系列答案| A. | 2 | B. | 3 | C. | 5 | D. | 7 |
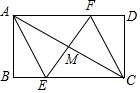 如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )| A. | AE=CF | B. | AB=AM | C. | AC⊥EF | D. | EF平分∠AEC |
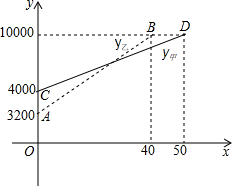 2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:
2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:
 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.