题目内容
7.如果a、b、c是非零有理数,且a+b+c=0,那么$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$+$\frac{abc}{|abc|}$的所有可能的值为0.分析 根据题意确定出a,b,c中负数的个数,原式利用绝对值的代数意义化简,计算即可得到结果.
解答 解:∵a、b、c为非零有理数,且a+b+c=0∴a、b、c只能为两正一负或一正两负.
①当a、b、c为两正一负时,设a、b为正,c为负,
原式=1+1+(-1)+(-1)=0,
②当a、b、c为一正两负时,设a为正,b、c为负
原式1+(-1)+(-1)+1=0,
综上,$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{{|{abc}|}}$的值为0,
故答案为:0.
点评 此题考查了绝对值,有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.下列正确的是( )
| A. | 若ac=bc,则a=b | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b | C. | 若a2=b2,则a=b | D. | 若|a|=|b|,则a=b |
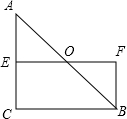 如图,在△ABC中,∠C=90°,点E是AC上的点,EF与AB相交于点O,且点O是AB的中点,AE=CE,BF∥AC,四边形BCEF是矩形吗?请说明理由.
如图,在△ABC中,∠C=90°,点E是AC上的点,EF与AB相交于点O,且点O是AB的中点,AE=CE,BF∥AC,四边形BCEF是矩形吗?请说明理由.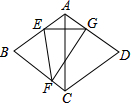 如图,在菱形ABCD中,∠BAD=120°,点E,F分别在AB,BC上,将△BEF沿EF折叠,点B落在AD上的点G处,EG⊥AC.
如图,在菱形ABCD中,∠BAD=120°,点E,F分别在AB,BC上,将△BEF沿EF折叠,点B落在AD上的点G处,EG⊥AC.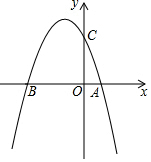 如图,已知抛物线y=-x2-2x+3与坐标轴分别交于A,B,C三点,在抛物线上找到一点D,使得∠DCB=∠ACO,则D点坐标为(-$\frac{5}{2}$,$\frac{7}{4}$)或(-4,-5).
如图,已知抛物线y=-x2-2x+3与坐标轴分别交于A,B,C三点,在抛物线上找到一点D,使得∠DCB=∠ACO,则D点坐标为(-$\frac{5}{2}$,$\frac{7}{4}$)或(-4,-5).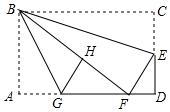 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论: