题目内容
 如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4
如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4| 2 |
| A、10 | B、16 | C、40 | D、80 |
考点:勾股定理的逆定理,全等三角形的性质,等腰直角三角形
专题:
分析:连结OO′.先由△CBO≌△ABO′,得出OB=O′B=4
,OC=O′A=10,∠OBC=∠O′BA,根据等式的性质得出∠O′BO=90°,由勾股定理得到O′O2=OB2+O′B2=32+32=64,则O′O=8.再利用勾股定理的逆定理证明OA2+O′O2=O′A2,得到∠AOO′=90°,那么根据S四边形AO′BO=S△AOO′+S△OBO′,即可求解.
| 2 |
解答: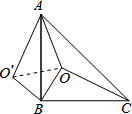 解:如图,连结OO′.
解:如图,连结OO′.
∵△CBO≌△ABO′,
∴OB=O′B=4
,OC=O′A=10,∠OBC=∠O′BA,
∴∠OBC+∠OBA=∠O′BA+∠OBA,
∴∠O′BO=90°,
∴O′O2=OB2+O′B2=32+32=64,
∴O′O=8.
在△AOO′中,∵OA=6,O′O=8,O′A=10,
∴OA2+O′O2=O′A2,
∴∠AOO′=90°,
∴S四边形AO′BO=S△AOO′+S△OBO′=
×6×8+
×4
×4
=24+16=40.
故选C.
 解:如图,连结OO′.
解:如图,连结OO′.∵△CBO≌△ABO′,
∴OB=O′B=4
| 2 |
∴∠OBC+∠OBA=∠O′BA+∠OBA,
∴∠O′BO=90°,
∴O′O2=OB2+O′B2=32+32=64,
∴O′O=8.
在△AOO′中,∵OA=6,O′O=8,O′A=10,
∴OA2+O′O2=O′A2,
∴∠AOO′=90°,
∴S四边形AO′BO=S△AOO′+S△OBO′=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故选C.
点评:本题考查了等腰直角三角形、全等三角形的性质,勾股定理及其逆定理,四边形的面积,难度适中,正确作出辅助线是解题的关键.

练习册系列答案
相关题目
如果一个多边形的内角和等于它的外角和,那么这个多边形是( )
| A、六边形 | B、五边形 |
| C、四边形 | D、三角形 |
 把一副三角板的直角顶点O重叠在一起.
把一副三角板的直角顶点O重叠在一起. 如图,网格中每个小正方形的边长为1,点C的坐标为(0,1).画出直角坐标系(要求标出x轴,y轴和原点)并写出点A、B的坐标.
如图,网格中每个小正方形的边长为1,点C的坐标为(0,1).画出直角坐标系(要求标出x轴,y轴和原点)并写出点A、B的坐标.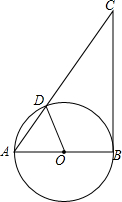 如图,△ABC中,∠C=30°,以AB为直径的⊙O交AC于点D,并且BC与⊙O相切,切点为B,
如图,△ABC中,∠C=30°,以AB为直径的⊙O交AC于点D,并且BC与⊙O相切,切点为B,
 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数