题目内容
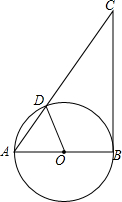 如图,△ABC中,∠C=30°,以AB为直径的⊙O交AC于点D,并且BC与⊙O相切,切点为B,
如图,△ABC中,∠C=30°,以AB为直径的⊙O交AC于点D,并且BC与⊙O相切,切点为B,(1)求∠ADO的度数;
(2)若AB=4
| 5 |
考点:切线的性质
专题:计算题
分析:(1)根据切线的性质得∠ABC=90°,再根据互余计算出∠A=90°-∠C=60°,然后利用OD=OA,根据等腰三角形的性质即可得到∠ADO=∠A=60°;
(2)先在Rt△ABC中根据含30度的直角三角形三边的关系得到AC=2AB=8
,再由∠ADO=∠A=60°判断△ADO为等边三角形,则AD=AO=
AB=2
,然后利用CD=AC-AD进行计算.
(2)先在Rt△ABC中根据含30度的直角三角形三边的关系得到AC=2AB=8
| 5 |
| 1 |
| 2 |
| 5 |
解答:解:(1)∵BC与⊙O相切,切点为B,
∴AB⊥BC,
∴∠ABC=90°,
∴∠A=90°-∠C=90°-30°=60°,
∵OD=OA,
∴∠ADO=∠A=60°;
(2)在Rt△ABC中,∵∠C=30°,
∴AC=2AB=2×4
=8
,
∵∠ADO=∠A=60°,
∴△ADO为等边三角形,
∴AD=AO=
AB=2
,
∴CD=AC-AD=8
-2
=6
.
∴AB⊥BC,
∴∠ABC=90°,
∴∠A=90°-∠C=90°-30°=60°,
∵OD=OA,
∴∠ADO=∠A=60°;
(2)在Rt△ABC中,∵∠C=30°,
∴AC=2AB=2×4
| 5 |
| 5 |
∵∠ADO=∠A=60°,
∴△ADO为等边三角形,
∴AD=AO=
| 1 |
| 2 |
| 5 |
∴CD=AC-AD=8
| 5 |
| 5 |
| 5 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
 如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4
如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4| 2 |
| A、10 | B、16 | C、40 | D、80 |
下列长度的各组线段中,能够组成直角三角形的是( )
| A、7,20,25 |
| B、8,15,17 |
| C、5,11,12 |
| D、5,6,7 |
 如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H. 如图,在Rt△ABC中,∠ACB=90°,且点B的坐标为(-2,0).画出△ABC绕点O顺时针旋转90°后的△A1B1C1,并求点B旋转时所扫过的面积(结果保留π).
如图,在Rt△ABC中,∠ACB=90°,且点B的坐标为(-2,0).画出△ABC绕点O顺时针旋转90°后的△A1B1C1,并求点B旋转时所扫过的面积(结果保留π).