题目内容
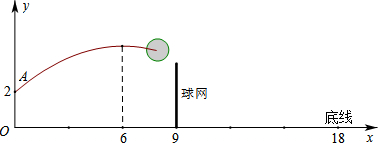
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h,已知球网与O点的水平距离为9m,球网高度为2.43m,球场另一边的底线距O点的水平距离为18m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出底线?请说明理由;
(3)若球一定能越过球网,且刚好落在底线上,求h的值.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出底线?请说明理由;
(3)若球一定能越过球网,且刚好落在底线上,求h的值.

考点:二次函数的应用
专题:
分析:(1)利用h=2.6将点(0,2),代入解析式求出即可;
(2)利用当x=9时,y=-
(x-6)2+2.6=2.45,当y=0时y=-
(x-6)2+2.6=0,分别得出即可;
(3)代入x=9和18得到有关h的方程求得h的值即可..
(2)利用当x=9时,y=-
| 1 |
| 60 |
| 1 |
| 60 |
(3)代入x=9和18得到有关h的方程求得h的值即可..
解答:解:(1)把x=0,y=2,及h=2.6代入到y=a(x-6)2+h
即2=a(0-6)2+2.6,
∴a=-
,
∴y=-
(x-6)2+2.6;
(2)h=2.6,y=-
(x-6)2+2.6
当x=9时,y=-
(9-6)2+2.6=2.45>2.43
∴球能越过网,
x=18时,y=-
(18-6)2+2.6=0.2>0
∴球会过界;
(3)x=0,y=2,代入到y=a(x-6)2+h得a=
;依题意:
x=9时,y=
(9-6)2+h=
>2.43 ①
x=18时,y=
(18-6)2+h=8-3h=0 ②
由①,②得h=
.
即2=a(0-6)2+2.6,
∴a=-
| 1 |
| 60 |
∴y=-
| 1 |
| 60 |
(2)h=2.6,y=-
| 1 |
| 60 |
当x=9时,y=-
| 1 |
| 60 |
∴球能越过网,
x=18时,y=-
| 1 |
| 60 |
∴球会过界;
(3)x=0,y=2,代入到y=a(x-6)2+h得a=
| 2-h |
| 36 |
x=9时,y=
| 2-h |
| 36 |
| 2+3h |
| 4 |
x=18时,y=
| 2-h |
| 36 |
由①,②得h=
| 8 |
| 3 |
点评:此题主要考查了二次函数的应用题,求范围的问题,可以利用临界点法求出自变量的值,再根据题意确定范围.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
下列说法正确的个数有( )
①射线AB与射线BA表示同一条射线.
②互余且相等的两个角都是45°.
③若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3.
④40°50ˊ=40.5°.
①射线AB与射线BA表示同一条射线.
②互余且相等的两个角都是45°.
③若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3.
④40°50ˊ=40.5°.
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4
如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4| 2 |
| A、10 | B、16 | C、40 | D、80 |
 如图,AD⊥BC,∠BAC≠90°,其中有几个直角三角形( )
如图,AD⊥BC,∠BAC≠90°,其中有几个直角三角形( )| A、3 | B、4 | C、5 | D、6 |
 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则从上面看到的该几何体的形状图的面积是
如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则从上面看到的该几何体的形状图的面积是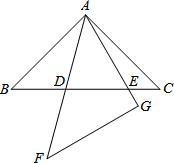 如图,△BAC、△AGF为等腰直角三角形,且△BAC≌△AGF,∠BAC=∠AGF=90°.若△BAC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E.请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
如图,△BAC、△AGF为等腰直角三角形,且△BAC≌△AGF,∠BAC=∠AGF=90°.若△BAC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E.请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.